Dynamic Pressure
Analysis of Pressure
An important property of any gas is its pressure. Because understanding what pressure is and how it works is so fundamental to the understanding of rocketry, we are including several slides on pressure in the Beginner’s Guide.
Two Perspectives to look at Pressure
There are two ways to look at pressure: (1) the small scale action of individual air molecules or (2) the large scale action of a large number of molecules. On the the small scale, from the kinetic theory of gases, a gas is composed of a large number of molecules that are very small relative to the distance between molecules. The molecules of a gas are in constant, random motion and frequently collide with each other and with the walls of any container. During collisions with the walls, there is a change in velocity and therefore a change in momentum of the molecules. The change in momentum produces a force on the walls which is related to the gas pressure. The pressure of a gas is a measure of the average linear momentum of the moving molecules of a gas. On the large scale, the pressure of a gas is a state variable, like the temperature and the density. The change in pressure during any process is governed by the laws of thermodynamics. Although pressure itself is a scalar quantity, we can define a pressure force to be equal to the pressure (force/area) times the surface area in a direction perpendicular to the surface. If a gas is static and not flowing, the measured pressure is the same in all directions. But if the gas is moving, the measured pressure depends on the direction of motion. This leads to the definition of the dynamic pressure.
Understanding Dynamic Pressure
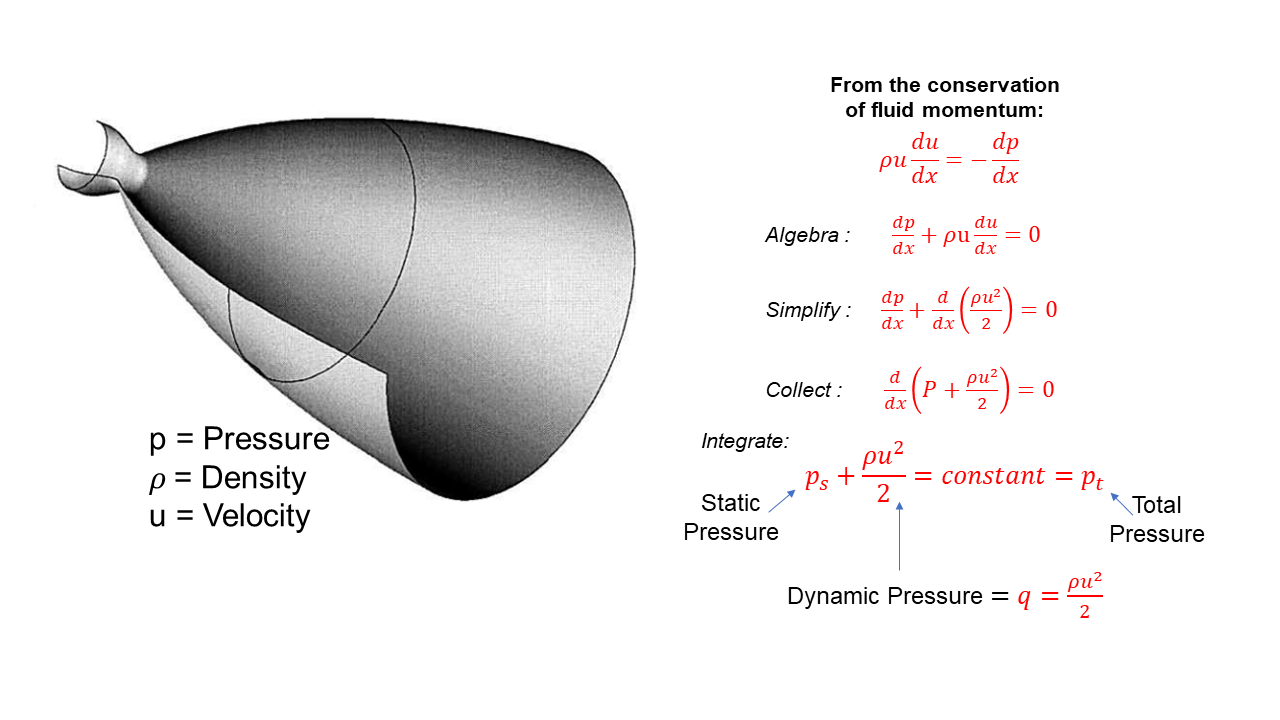
To understand dynamic pressure, we begin with a one dimensional version of the conservation of linear momentum for a fluid.
\(\LARGE \rho\frac{\text{d}u}{\text{d}x}=-\frac{\text{d}p}{\text{d}x}\)
where rho (\(\bf\rho\)) is the density of the gas, p is the pressure, x is the direction of the flow, and u is the velocity in the x direction. Performing a little algebra:
\(\LARGE \frac{\text{d}p}{\text{d}x}+\rho u\frac{\text{d}u}{\text{d}x}=0\)
For a constant density (incompressible flow) we can take the “\(\rho u\)” term inside the differential:
\(\LARGE \frac{\text{d}p}{\text{d}x}+\frac{\text{d}}{\text{d}x}(\frac{\rho u^{2}}{2})=0\)
and then gather all of the terms:
\(\LARGE \frac{\text{d}}{\text{d}x}(P+\frac{\rho u^{2}}{2})=0\)
Integrating this differential equation:
\(\LARGE p_{s}+\frac{\rho u^{2}}{2}=\text{constant}=p_{t}\)
This equation looks exactly like the incompressible form of Bernoulli’s equation. Each term in this equation has the dimensions of a pressure (force/area); ps is the static pressure, the constant pt is called the total pressure, and
\(\LARGE \frac{1}{2}\rho u^{2}\)
is called the dynamic pressure because it is a pressure term associated with the velocity u of the flow. Dynamic pressure is often assigned the letter q in aerodynamics:
\(\LARGE q=\frac{1}{2}\rho u^{2}\)
Manipulating Pressure
The dynamic pressure is a defined property of a moving flow of gas. We have performed this simple derivation to determine the form of the dynamic pressure, but we can use and apply the idea of dynamic pressure in much more complex flows, like compressible flows or viscous flows. In particular, the aerodynamic forces acting on an object as it moves through the air are directly proportional to the dynamic pressure. The dynamic pressure is therefore used in the definition of the lift coefficient and the drag coefficient. As we have seen, dynamic pressure appears in Bernoulli’s equation even though that relationship was originally derived using energy conservation.
Dependencies of Dynamic Pressure
The dynamic pressure depends on both the local value of the density and the velocity of the flow, or rocket. The density of the air decreases with altitude in a complex manner. The velocity of a rocket during launch is constantly increasing with altitude. Therefore, the dynamic pressure on a rocket during launch is initially zero because the velocity is zero. The dynamic pressure increases because of the increasing velocity to some maximum value, called the maximum dynamic pressure, or Max Q. Then the dynamic pressure decreases because of the decreasing density. The Max Q condition is a design constraint on full scale rockets. You can investigate the variation of dynamic pressure with altitude and velocity by using our atmosphere simulator.