Gas Temperature
Temperature
An important property of any gas is temperature. We have some experience with temperature that we don’t have with properties like viscosity and compressibility. We’ve heard the TV meteorologist give the daily value of the temperature of the atmosphere (15 degrees Celsius, for example). We know that a hot object has a high temperature, and a cold object has a low temperature. And we know that the temperature of an object can change if we heat the object or cool it.
Fragile Prescription on Temperature
Scientists, however, must be more precise than simply describing an object as “hot” or “cold.” An entire branch of physics, called thermodynamics, is devoted to studying the temperature of objects and the transfer of heat between objects of different temperatures. We are including some fundamentals of thermodynamics in the Beginner’s Guide to help you better understand rocket propulsion. We are also including an interactive simulator to let you study how temperature varies with height through the atmosphere.
The Two Modes of Temperature
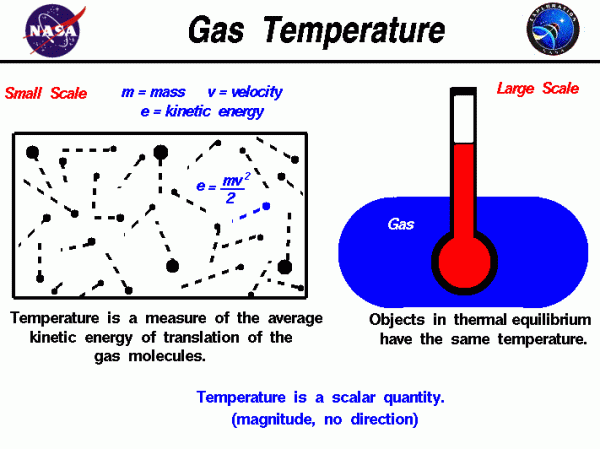
There are two ways to look at temperature: (1) the small-scale action of individual air molecules and (2) the large-scale action of the gas as a whole. Starting with the small-scale action, from the kinetic theory of gases, a gas is composed of a large number of molecules that are very small relative to the distance between molecules. The molecules are in constant, random motion and frequently collide with each other and with the walls of any container. The molecules possess the physical properties of mass, momentum, and energy. The momentum of a single molecule is the product of its mass and velocity, while the kinetic energy is one half the mass times the square of the velocity, as shown on the left of the above figure.
For diatomic gases like oxygen and nitrogen, in which the molecules are composed of pairs of atoms, energy can also be stored in the vibration and rotation of the atoms about each other. The temperature of a gas is a measure of the average translational kinetic energy of the molecules. In a hot gas, the molecules move faster than in a cold gas; the mass remains the same, but the kinetic energy, and hence the temperature, is greater because of the increased velocity of the molecules.
Turning to the Larger Scale
The temperature of a gas is something that we can determine qualitatively with our senses. We can sense that one gas is hotter than another gas and therefore has a higher temperature. But to determine the temperature quantitatively, to assign a number, we must use some principles from thermodynamics:
- The first principle is the observation that the temperature of an object can affect some physical property of the object, such as the length of a solid, or the gas pressure in a closed vessel, or the electrical resistance of a wire. You can explore the effects of temperature on the pressure of a gas at the animated gas lab.
- The second principle is the definition of thermodynamic equilibrium between two objects. Two objects are in thermodynamic equilibrium when they have the same temperature.
- And the final principle is the observation that if two objects of different temperatures are brought into contact with one another, they will eventually establish a thermodynamic equilibrium. The word “eventually” is important. Insulating materials reach equilibrium after a very long time, while conducting materials reach equilibrium very quickly.
Temperature Scales
With these three thermodynamic principles, we can construct a device for measuring temperature, a thermometer, which assigns a number to the temperature of an object. When the thermometer is brought into contact with another object, it quickly establishes a thermodynamic equilibrium. By measuring the thermodynamic effect on some physical property of the thermometer at some fixed conditions, like the boiling point and freezing point of water, we can establish a scale for assigning temperature values.
The number assigned to the temperature depends on what we pick for the reference condition. So, several different temperature scales have arisen. The Celsius scale, designated with a C, uses the freezing point of pure water as the zero point and the boiling point as 100 degrees with a linear scale in between these extremes. The Fahrenheit scale, designated with an F, is a lot more confusing. It originally used the freezing point of sea water as the zero point and the freezing point of pure water as 30 degrees, which made the temperature of a healthy person equal to 96 degrees. On this scale, the boiling point of pure water was 212 degrees.
So, Fahrenheit adjusted the scale to make the boiling point of pure water 212 and the freezing point of pure water 32, which gave 180 degrees between the two reference points. 180 degrees was chosen because it is evenly divisible by 2, 3, 4, 5, and 6. On the new temperature scale, the temperature of a healthy person is 98.6 degrees F. Because there are 100 degrees C and 180 degrees F between the same reference conditions:
\(\LARGE 1^{\circ}C=1^{\circ}F\times\frac{100}{180}=1^{\circ}F\times\frac{5}{9}\)
Since the scales start at different zero points, we can convert from the temperature on the Fahrenheit scale (TF) to the temperature on the Celsius scale (TC) by using this equation:
\(\LARGE \mathit{TF}=32+\frac{9}{5}\mathit{TC}\)
Of course, you can have temperatures below the freezing point of water, and these are assigned negative numbers. When scientists began to study the coldest possible temperature, they determined an absolute zero at which molecular kinetic energy is a minimum (but not strictly zero!). They found this value to be at -273.16 degrees C. Using this point as the new zero point we can define another temperature scale called the absolute temperature. If we keep the size of a single degree to be the same as the Celsius scale, we get a temperature scale which has been named after Lord Kelvin and designated with a K. Then:
\(\LARGE K=C+273.16\)
There is a similar absolute temperature corresponding to the Fahrenheit degree. It is named after the scientist Rankine and designated with an R.
\(\LARGE R=F+459.69\)
Absolute temperatures are used in the equation of state, the derivation of the state variables enthalpy, and entropy, and determining the speed of sound.
Temperature, like pressure, is a scalar quantity. Temperature has a magnitude, but no direction associated with it. It has just a single value at every location in a gas. The value can change from location to location, but there is no direction connected to the temperature.