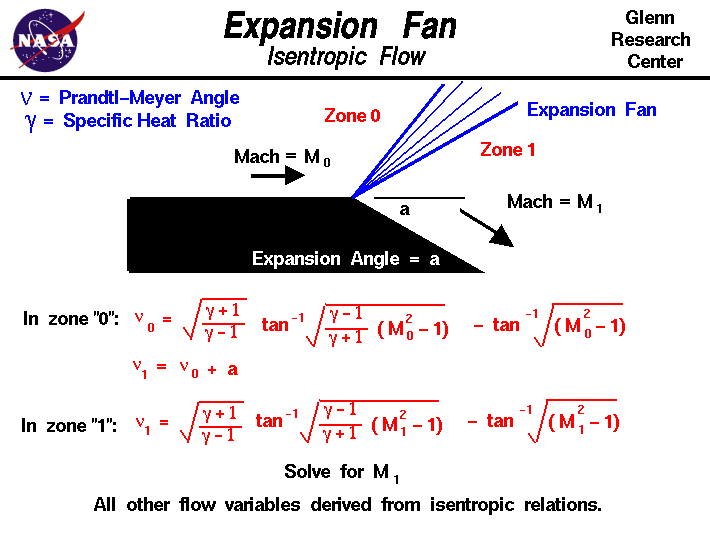
Centered Expansion Fan

As an object moves through a gas, the gas molecules are deflected around the object. If the speed of the object is much less than the speed of sound of the gas, the density of the gas remains constant, and the flow of gas can be described by conserving momentum and energy. As the speed of the object increases towards the speed of sound, we must consider compressibility effects on the gas. The density of the gas varies locally as the gas is compressed by the object. When an object moves faster than the speed of sound, and there is an abrupt decrease in the flow area, shock waves are generated. If the flow area increases, however, a different flow phenomenon is observed. If the increase is abrupt, we encounter a centered expansion fan. The word “expansion” denotes that the area is increasing.

There are some marked differences between shock waves and expansion fans. Across a shock wave, the Mach number decreases, the static pressure increases, and there is a loss of total pressure because the process is irreversible. Through an expansion fan, the Mach number increases, the static pressure decreases, and the total pressure remains constant. Expansion fans are isentropic.

Calculating the Expansion Fan

The calculation of the expansion fan involves the use of the Prandtl-Meyer function. This function is derived from conservation of mass, momentum, and energy for very small (differential) deflections. The Prandtl-Meyer function is denoted by the Greek letter nu (\(\bf \nu\)) on the slide and is a function of the Mach number M and the ratio of specific heats gam (\(\bf \gamma\)) of the gas.

The physical interpretation of the Prandtl-Meyer function is that it is the angle through which you must expand a sonic (M=1) flow to obtain a given Mach number. To compute an expansion from some other Mach number, we denote the upstream conditions as zone “0” and we calculate the Prandtl-Meyer angle for that Mach number.

\(\LARGE \nu_0=\sqrt{\frac{\gamma+1}{\gamma-1}}\tan^{-1}{(\sqrt\frac{\gamma-1)(M_{0}^{2}-1)}{\gamma+1}})-\tan^{-1}(\sqrt{M_{0}^{2}-1})\)

where tan^-1 is the trigonometric inverse tangent function. The meaning of tan^-1 can be explained by these two equations:

\(\LARGE \tan^{-1}a=b\)

\(\LARGE \tan b=a\)

We then add the expansion angle a to get the value of the Prandtl-Meyer function in zone “1”.

\(\LARGE \nu_{1}=\nu_{0}+a\)

Then we must iterate (or look up in a table) to obtain the Mach number in zone “1” which gives that value of the Prandtl-Meyer function.

\(\LARGE \nu_1=\sqrt{\frac{\gamma+1}{\gamma-1}}\tan^{-1}{(\sqrt\frac{\gamma-1)(M_{1}^{2}-1)}{\gamma+1}})-\tan^{-1}(\sqrt{M_{1}^{2}-1})\)

Knowing the Mach number in zone “1” and knowing that the flow is isentropic, we can relate the value of all the flow variables in zone “1” to the variables in zone “0” through the ratio to the total conditions given on the isentropic flow page.

The centered expansion shown on this slide is a special case of the distributed expansion. Flow expansions can be generated over a long distance as well as over the sharp edge as noted on the slide. Since the flow is isentropic, it is reversible. Under very careful conditions, we can create isentropic compressions which take a high Mach number flow down to low Mach numbers and increase the static pressure without the loss of total pressure associated with shock waves. Isentropic compression inlets have been designed for high-speed flows, but typically remain isentropic only over a narrow operating range. If the free stream Mach number is changed, the isentropic compression waves often coalesce into a shock wave with the accompanying loss in total pressure.

The Expansion Fan Problem

Here is a Java program which solves the expansion fan problem.

Please note: the simulation below is best viewed on a desktop computer. It may take a few minutes for the simulation to load.

General Instructions

To study the expansion fan, you can choose from two types of problems: the default problem assumes that you know the angle of expansion and wish to solve for the flow downstream of the expansion; the alternate problem assumes that you have a specified pressure ratio, and you wish to determine the angle of the expansion and the other flow variables. Input to the program is made using the sliders, or input boxes at the lower left. To change the value of an input variable, simply move the slider or click on the input box, select and replace the old value to send the new value to the program.

Output from the program is displayed in output boxes at the lower right. The flow variables are presented as ratios to the free stream value (0). The graphic at the top shows the expansion surface in red and the initial and terminal waves generated by the surface as lines. The user can move the display by clicking on the graphic, holding down, and dragging the graphic. You can zoom in or out of the graphic by using the slider at the left. If you lose the graphic, click on “Find” to restore the initial display.