Speed of Sound Interactive

Image of speed of sound

Speed of Sound

Air is a gas, and an important property of any gas is the speed of sound through the gas. Why are we interested in the speed of sound? The speed of “sound” is the speed of transmission of a small disturbance through a medium. Sound itself is a sensation created in the human brain in response to sensory inputs from the inner ear. (We won’t comment on the old “tree falling in a forest” discussion!)

Isentropic Process

Disturbances are transmitted through a gas as a result of collisions between the randomly moving molecules in the gas. The transmission of a small disturbance through a gas is an isentropic process. The conditions in the gas are the same before and after the disturbance passes through. Because the speed of transmission depends on molecular collisions, the speed of sound depends on the state of the gas.

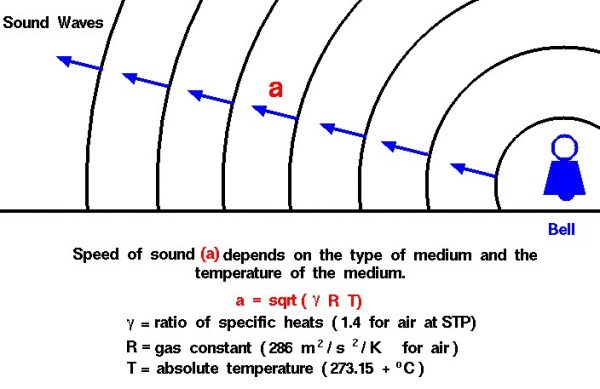
The speed of sound is a constant within a given gas and the value of the constant depends on the type of gas (air, pure oxygen, carbon dioxide, etc.) and the temperature of the gas. An analysis based on conservation of mass and momentum shows that the speed of sound a is equal to the square root of the ratio of specific heat gamma (\(\bf\gamma\)) times the gas constant R times the temperature T.

\(\LARGE a=\sqrt{gRT}\)

Temperature

Notice that the temperature must be specified on an absolute scale (Kelvin or Rankine). The dependence on the type of gas is included in the gas constant R. which equals the universal gas constant divided by the molecular weight of the gas, and the ratio of specific heats.

The speed of sound in air depends on the type of gas and the temperature of the gas. On Earth, the atmosphere is composed of mostly diatomic nitrogen and oxygen, and the temperature depends on the altitude in a rather complex way. Scientists and engineers have created a mathematical model of the atmosphere to help them account for the changing effects of temperature with altitude.

Mars also has an atmosphere composed of mostly carbon dioxide. There is a similar mathematical model of the Martian atmosphere. We have created an atmospheric calculator to let you study the variation of sound speed with planet and altitude.

Speed of Sound Simulation

Here is a JavaScript program to calculate the speed of sound and Mach number for different planets, altitudes, and speed. You can use this calculator to determine the Mach number of a rocket at a given speed and altitude on Earth or Mars.

Please note: the simulation below is best viewed on a desktop computer. It may take a few minutes for the simulation to load.

General Instructions

To change input values, click on the input box, backspace over the input value, type in your new value, and hit the Enter key on the keyboard (this sends your new value to the program). You will see the output boxes change value. You can use either English or Metric units and you can input either the Mach number or the speed by using the menu buttons. Just click on the menu button and click on your selection. There is a sleek version of this program for experienced users who do not need these instructions.

Mach Number

As an object moves through the atmosphere, the air is disturbed and the disturbances are transmitted through the air at the speed of sound. You can study how the disturbances are transmitted with an interactive sound wave simulator. If we consider the atmosphere on a standard day at sea level static conditions, the speed of sound is about 761 mph or 1100 feet/second. We can use this knowledge to approximately determine how far away a lightning strike has occurred.

Aircraft and Speed

The speed of sound in the atmosphere is a constant that depends on the altitude, but an aircraft can move through the air at any desired speed. The ratio of the aircraft’s speed to the speed of sound affects the forces on the aircraft. Aeronautical engineers call the ratio of the aircraft’s speed to the speed of sound the Mach number, M. If the aircraft moves much slower than the speed of sound, conditions are said to be subsonic, 0 < M << 1, and compressibility effects are small and can be neglected. If the aircraft moves near the speed of sound, conditions are said to be transonic, M ~ 1, and compressibility effects like flow choking become very important.

For aircraft speeds greater than the speed of sound, conditions are said to be supersonic, 1 < M < 3, and compressibility effects are important. Depending on the specific shape and speed of the aircraft, shock waves may be produced in the supersonic flow of gas.

For high supersonic speeds, 3 < M < 5, aerodynamic heating becomes very important. If the aircraft moves more than five times the speed of sound, conditions are said to be hypersonic, M > 5, and the high energy involved under these conditions have significant effects on the air itself. The Space Shuttle re-enters the atmosphere at high hypersonic speeds, M ~ 25. Under these conditions, the heated air becomes an ionized plasma of gas and the spacecraft must be insulated from the high temperatures.