Oblique Shocks Interactive Simulator
Speed of an Object
As an object moves through a gas, the gas molecules are deflected around the object. If the speed of the object is much less than the speed of sound of the gas, the density of the gas remains constant and the flow of gas can be described by conserving momentum, and energy. As the speed of the object approaches the speed of sound, we must consider compressibility effects on the gas. The density of the gas varies locally as the gas is compressed by the object.
Compressible Flow
For compressible flows with little or small flow turning, the flow process is reversible, and the entropy is constant. The change in flow properties is then given by the isentropic relations (isentropic means “constant entropy”). But when an object moves faster than the speed of sound, and there is an abrupt decrease in the flow area, shock waves are generated in the flow.
Shock waves are very small regions in the gas where the gas properties change by a large amount. Across a shock wave, the static pressure, temperature, and gas density increase almost instantaneously. The changes in the flow properties are irreversible and the entropy of the entire system increases. Because a shock wave does no work, and there is no heat addition, the total enthalpy and the total temperature are constant. But because the flow is non-isentropic, the total pressure downstream of the shock is always less than the total pressure upstream of the shock.
There is a loss of total pressure associated with a shock wave as shown on the figure. Because total pressure changes across the shock, we cannot use the usual (incompressible) form of Bernoulli’s equation across the shock. The Mach number and speed of the flow also decrease across a shock wave.
Shock Waves
If the shock wave is perpendicular to the flow direction, it is called a normal shock. Some equations describe the change in the flow variables. The equations are derived from the conservation of mass, momentum, and energy. Depending on the shape of the object and the speed of the flow, the shock wave may be inclined to the flow direction. When a shock wave is inclined to the flow direction it is called an oblique shock.
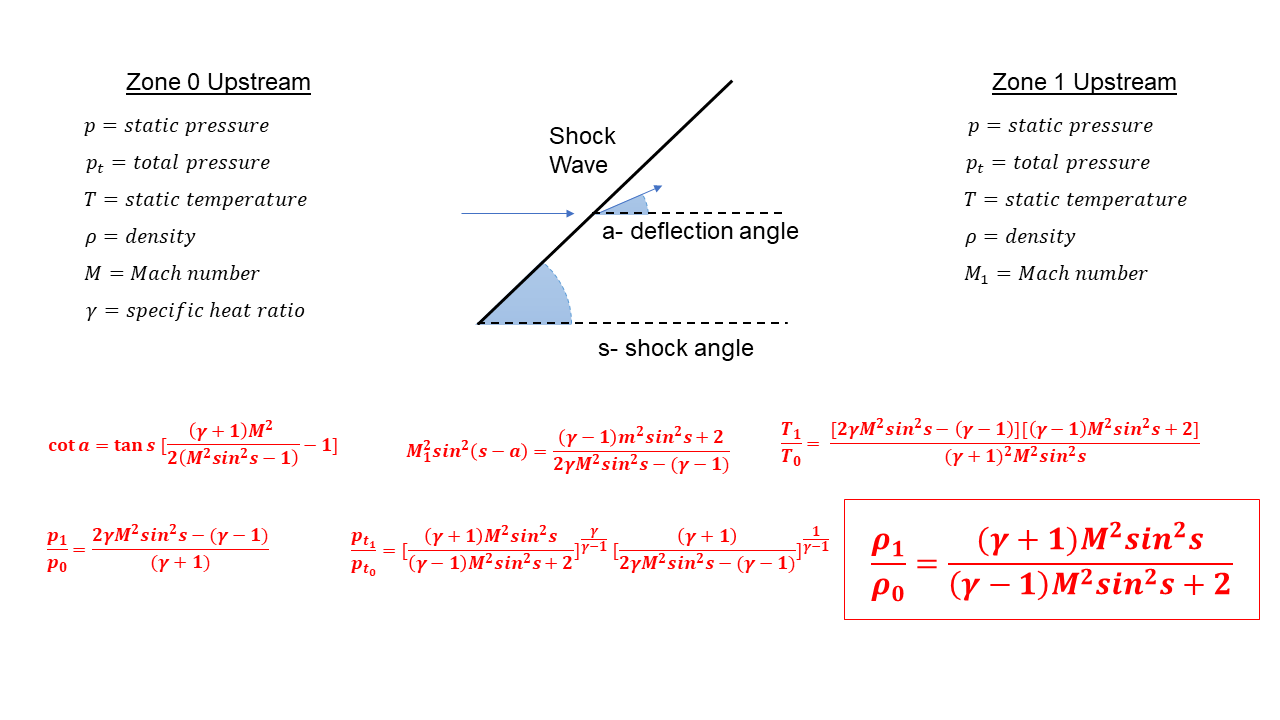
On the figure, we have listed the equations which describe the change in flow variables for flow across an oblique shock. The equations presented here were derived by considering the conservation of mass, momentum, and energy for a compressible gas while ignoring viscous effects. These have been further specialized for a two-dimensional flow without heat addition.
The equations only apply for those combinations of free-stream Mach number and deflection angle for which an oblique shock occurs. If the deflection is too high, or the Mach too low, a normal shock occurs. For the Mach number change across an oblique shock there are two possible solutions: one supersonic and one subsonic. In nature, the supersonic (“weak shock”) solution occurs most often. However, under some conditions the “strong shock”, a subsonic solution is possible.
Oblique Shocks
Oblique shocks are generated by the nose and by the leading edge of the wing and tail of a supersonic aircraft. Oblique shocks are also generated at the trailing edges of the aircraft as the flow is brought back to free stream conditions. Oblique shocks also occur downstream of a nozzle if the expanded pressure is different from free stream conditions. In high-speed inlets, oblique shocks are used to compress the air going into the engine. The air pressure is increased without using any rotating machinery.
Deflection Angle
On the slide, a supersonic flow at Mach number M approaches a shock wave which is inclined at angle s. The flow is deflected through the shock by an amount specified as the deflection angle – a. The deflection angle is determined by resolving the incoming flow velocity into components parallel and perpendicular to the shock wave. The component parallel to the shock is assumed to remain constant across the shock, the component perpendicular is assumed to decrease by the normal shock relations. Combining the components downstream of the shock determines the deflection angle. Then:
\(\LARGE \cot(a)=\tan(s)[\frac{(y+1)M^{2}}{2(M^{2}\sin^{2}(s)-1)}-1]\)
where tan is the trigonometric tangent function, cot is the co-tangent function:
\(\LARGE \cot (a)=\tan(90^{\circ}-a)\)
and sin2 is the square of the sine. Gam (\(\bf\gamma\)) is the ratio of specific heats. Across the shock wave the Mach number decreases to a value specified as M1:
\(\LARGE M_{1}^{2}\sin^{2}(s-a)=\frac{(y-1)m^{2}\sin^{2}(s)+2}{2\gamma M^{2}\sin^{2}s-(\gamma-1)}\)
The total temperature across the shock is constant, but the static temperature T increases in zone 1 to become:
\(\LARGE \frac{T_{1}}{T_{0}}=\frac{[2\gamma M^{2}\sin^{2}(s)-(\gamma-1)][(\gamma-1)M^{2}\sin^{2}s+2]}{(\gamma+1)^{2}M^{2}\sin^{2}(s)}\)
The total pressure pt decreases according to:
\(\LARGE \frac{p_{t_{1}}}{p_{t_{0}}}=[\frac{(\gamma+1)M^{2}sin^{2}(s)}{(\gamma-1)M^{2}\sin^{2}(s)+2}]^{\frac{\gamma}{\gamma-1}}[\frac{\gamma+1}{2\gamma M^{2}\sin^{2}(s)-(\gamma-1)}]^\frac{1}{\gamma-1}\)
The static pressure p increases to:
\(\LARGE \frac{p_{1}}{p_{0}}=\frac{2\gamma M^{2}\sin^{2}(s)-(\gamma-1)}{\gamma+1}\)
And the density rho (\(\bf\rho\)) changes by:
\(\LARGE \frac{\rho_{1}}{\rho_{0}}=\frac{(\gamma+1)M^{2}\sin^{2}(s)}{(\gamma-1)M^{2}\sin^{2}(s)+2}\)
Shock Angle
The right-hand side of all these equations depends only on the free-stream Mach number and the shock angle. The shock angle depends in a complex way on the free-stream Mach number and the wedge angle. So, knowing the Mach number and the wedge angle, we can determine all the conditions associated with the oblique shock. The equations describing oblique shocks were published in the NACA report (NACA-1135) in 1951.
Here is a Java program based on the oblique shock equations. You can use this simulator to study the flow past a wedge.
Please note: the simulation below is best viewed on a desktop computer. It may take a few minutes for the simulation to load.
General Instructions
Input to the program can be made using the sliders, or input boxes at the upper right. To change the value of an input variable, simply move the slider. Or click on the input box, select and replace the old value, and hit Enter to send the new value to the program. Output from the program is displayed in output boxes at the lower right. The flow variables are presented as ratios to free stream values. The graphic at the left shows the wedge (in red) and the shock wave generated by the wedge as a line. The line is colored blue for an oblique shock and magenta when the shock is normal. The black lines show the streamlines of the flow past the wedge. Notice that downstream (to the right) of the shock wave, the lines are closer together than upstream. This indicates an increase in the density of the flow.
There is a more complete shock simulation program that is available on this website. The program solves for flow past a wedge and for flow past a cone, including the detached normal shock conditions. Another simulation, called ShockModeler, describes the intersection and reflection of multiple shock waves.