Normal Shocks Interactive
Speed of an Object
As an object moves through a gas, the gas molecules are deflected around the object. If the speed of the object is much less than the speed of sound of the gas, the density of the gas remains constant, and the flow of gas can be described by conserving momentum and energy. As the speed of the object increases towards the speed of sound, we must consider compressibility effects on the gas. The density of the gas varies locally as the gas is compressed by the object.
Flow Properties
For compressible flows with little or small flow turning, the flow process is reversible and the entropy is constant. The change in flow properties are then given by the isentropic relations (isentropic means “constant entropy”). But when an object moves faster than the speed of sound, and there is an abrupt decrease in the flow area, the flow process is irreversible and the entropy increases. Shock waves are generated which are very small regions in the gas where the gas properties change by a large amount.
Across a shock wave, the static pressure, temperature, and gas density increases almost instantaneously. The Mach number and speed of the flow decrease across a shock wave. If the upstream Mach number is in the low supersonic regime, the specific heat ratio of air remains a constant value (1.4) and air is said to be calorically perfect. But under low hypersonic flow conditions or high total temperature conditions, the specific heat ratio changes and air is then said to be calorically imperfect. Derived flow variables, like the speed of sound and the isentropic flow relations are slightly different for a calorically imperfect gas than the conditions predicted for a calorically perfect gas because some of the energy of the flow excites the vibrational modes of the diatomic molecules of nitrogen and oxygen in the air.
Shock Wave
Because a shock wave does not work, and there is no heat addition, the total enthalpy and the total temperature are constant through the shock. But because the flow is non-isentropic, the total pressure downstream of the shock is always less than the total pressure upstream of the shock; there is a loss of total pressure associated with a shock wave. The ratio of the total pressure is shown on the slide. Because total pressure changes across the shock, we cannot use the usual (incompressible) form of Bernoulli’s equation across the shock.
Normal Shock
If the shock wave is perpendicular to the flow direction it is called a normal shock. On this web page, we have listed the equations which describe the change in flow variables for flow across a normal shock. There are two groups of equations and two slides: one for the calorically perfect gas, and the other for the calorically imperfect gas. The equations presented here were derived by considering the conservation of mass, momentum, and energy. for a compressible gas while ignoring viscous effects. The equations have been further specialized for a one-dimensional flow without heat addition.
Mach Number
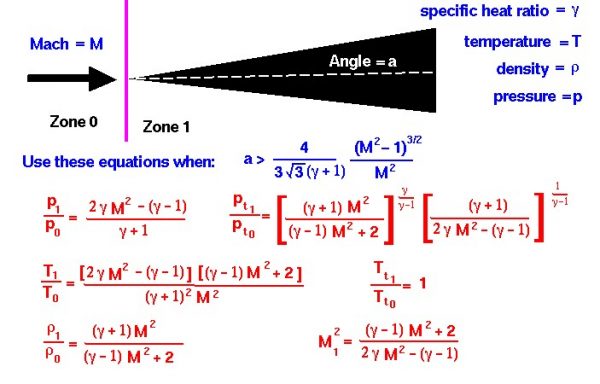
The equations can be applied to the two-dimensional flow past a wedge for the following combination of free stream Mach number M and wedge angle a:
\(\LARGE a>\frac{4}{3\sqrt{3}(\gamma+1)}\frac{(M^{2}-1)^{\frac{3}{2}}}{M^{2}}\)
where gam (\(\bf\gamma\)) is the ratio of specific heats. If the wedge angle is less than this detachment angle, an attached oblique shock occurs, and the equations are slightly modified.
Beginning with the calorically perfect gas, across the normal shock wave the Mach number decreases to a value specified as M1:
\(\LARGE M_{1}^{2}=\frac{(\gamma-1)M^{2}+2}{2\gamma M^{2}-(\gamma-1)}\)
The total temperature Tt across the shock is constant,
\(\LARGE \frac{T_{t_{1}}}{T_{t_{0}}}=1\)
The static temperature T increases in zone 1 to become:
\(\LARGE \frac{T_{1}}{T_{0}}=\frac{[2\gamma M^{2}-(\gamma-1)][(\gamma-1)M^{2}+2]}{(\gamma+1)^{2}M^{2}}\)
The static pressure p increases to:
\(\LARGE \frac{p_{1}}{p_{0}}=\frac{2\gamma M^{2}-(\gamma-1)}{\gamma+1}\)
And the density rho (\(\bf\rho\)) changes by:
\(\LARGE \frac{\rho_{1}}{\rho_{0}}=\frac{(\gamma+1)M^{2}}{(\gamma-1)M^{2}+2}\)
The total pressure pt decreases according to:
\(\LARGE \frac{p_{t_{1}}}{p_{t_{0}}}=[\frac{\gamma+1)M^{2}}{(\gamma-1)M^{2}+2}]^{\frac{\gamma}{\gamma-1}}[\frac{\gamma+1}{2\gamma M^{2}-(\gamma-1)}]^{\frac{1}{\gamma-1}}\)
The right-hand side of all these equations depend only on the free stream Mach number. So, knowing the Mach number, we can determine all the conditions associated with the normal shock. The equations describing normal shocks were published in a NACA report (NACA-1135) in 1951.
Now, turning to the calorically imperfect gas, the procedure for determining the conditions across a normal shock are much more complicated than the procedure for the calorically perfect gas. Mathematical models based on a simple harmonic vibrator have been developed for the calorically imperfect gas. The details of the analysis were given by Eggars in NACA Report 959. A synopsis of the report is included in NACA-1135. A collection of the equations and a description of the method is shown on this slide:
As with the calorically perfect case, the conservation of mass, momentum, and energy equations are solved simultaneously to determine the flow conditions across the normal shock. For the calorically imperfect case, additional terms are added to the energy equation to account for the vibration of the molecules at high temperatures. The resulting equation for the static temperature downstream of the shock is:
\(\Large (u+\frac{RT}{u})^{2}-(u+\frac{RT}{u})\sqrt{(u+\frac{RT}{u})^{2}-4RT_{1}}-2RT_{1}-2u^{2}\\\Large+\frac{\gamma_{\text{perf}}}{\gamma_{\text{perf}}-1}4R(T_{1}-T)+4R^{\theta}(\frac{1}{e^{\frac{\theta}{T_{1}}}-1}-\frac{1}{e^{\frac{\theta}{T}}-1})=0\)
where R is the gas constant, u is the upstream velocity, T is the upstream static temperature, T1 is the downstream static temperature, theta (\(\bf\theta\)) is a constant equal to 5500 Rankine, and gam (\(\bf\gamma\)) is the calorically perfect ratio of specific heats. There is no known direct solution to this equation, so it must be solved iteratively for the downstream temperature.
Having the downstream static temperature, we can use the calorically imperfect isentropic relations upstream and downstream of the shock to determine all of the other variables. Total temperature remains a constant across the shock wave. We have listed some of the isentropic ratios on the slide which must also be solved iteratively.
Here’s a Java program that solves the normal shock equations for the calorically perfect and the calorically imperfect conditions:
General Instructions
To change input values, click on the input box, backspace over the input value, type in your new value. Then hit the red COMPUTE button to send your new value to the program. You will see the output boxes change value. You can use either Imperial or Metric units. Just click on the menu button and click on your selection. For the given altitude input, the program computes the upstream standard day conditions. The ratios are computed using the Mach number and specific heat ratio inputs and the equations given in the figure. The downstream conditions are computed from the upstream conditions and the ratios. If you are an experienced user of this simulator, you can use a sleek version of the program which loads faster on your computer and does not include these instructions.
Please note: the simulation below is best viewed on a desktop computer. It may take a few minutes for the simulation to load.
There is a more complete shock simulation program that is also available at this web site. The ShockModeler program models the intersection and reflection of multiple shock waves.