Boundary Layer
Aerodynamic Force
As an object moves through a fluid, or as a fluid moves past an object, the molecules of the fluid near the object are disturbed and move around the object. Aerodynamic forces are generated between the fluid and the object. The magnitude of these forces depends on the shape of the object, the speed of the object, the mass of the fluid going by the object and on two other important properties of the fluid: the viscosity, or stickiness, and the compressibility, or springiness, of the fluid. To properly model these effects, aerospace engineers use similarity parameters which are ratios of these effects to other forces present in the problem. If two experiments have the same values for the similarity parameters, then the relative importance of the forces are being correctly modeled.
Viscosity of a Fluid
Aerodynamic forces depend in a complex way on the viscosity of the fluid. As the fluid moves past the object, the molecules right next to the surface stick to the surface. The molecules just above the surface are slowed down in their collisions with the molecules sticking to the surface. These molecules in turn slow down the flow just above them. The farther one moves away from the surface, the fewer the collisions affected by the object surface. This creates a thin layer of fluid near the surface in which the velocity changes from zero at the surface to the free stream value away from the surface. Engineers call this layer the boundary layer because it occurs on the boundary of the fluid.
Boundary Layer
The details of the flow within the boundary layer are very important for many problems in aerodynamics, including wing stall, the skin friction drag on an object, and the heat transfer that occurs in high-speed flight. Unfortunately, the physical and mathematical details of boundary layer theory are beyond the scope of this beginner’s guide and are usually studied in late undergraduate or graduate school in college. We will only present some of the effects of the boundary layer at this time.
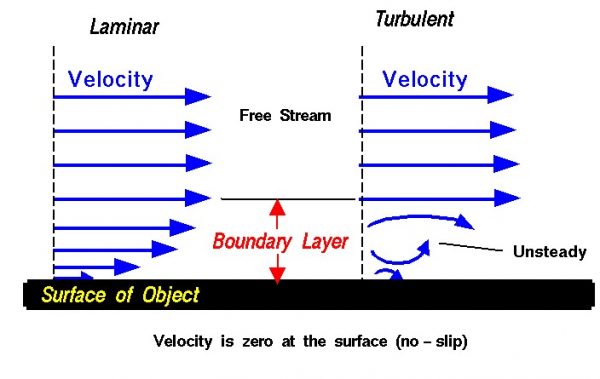
Velocity
On the slide we show the stream wise velocity variation from free stream to the surface. In reality, the effects are three dimensional. From the conservation of mass in three dimensions, a change in velocity in the stream wise direction causes a change in velocity in the other directions as well. There is a small component of velocity perpendicular to the surface which displaces or moves the flow above it. One can define the thickness of the boundary layer to be the amount of this displacement. The displacement thickness depends on the Reynolds number, which is the ratio of inertial (resistant to change or motion) forces to viscous (heavy and gluey) forces and is given by the equation: Reynolds number (Re) equals velocity (V) times density (rho, \(\rho\)) times a characteristic length (l) divided by the viscosity coefficient (mu, \(\mu\)).
\(\LARGE \mathit{Re}=\frac{V\rho l}{\mu}\)
Reynolds Number
Boundary layers may be either laminar (layered), or turbulent (disordered) depending on the value of the Reynolds number. For lower Reynolds numbers, the boundary layer is laminar and the streamwise velocity changes uniformly as one moves away from the wall, as shown on the left side of the figure. For higher Reynolds numbers, the boundary layer is turbulent and the streamwise velocity is characterized by unsteady (changing with time) swirling flows inside the boundary layer. The external flow reacts to the edge of the boundary layer just as it would to the physical surface of an object.
So, the boundary layer gives any object an “effective” shape which is usually slightly different from the physical shape. To make things more confusing, the boundary layer may lift off or “separate” from the body and create an effective shape much different from the physical shape. This happens because the flow in the boundary has very low energy (relative to the free stream) and is more easily driven by changes in pressure. Flow separation is the reason for wing stall at high angle of attack. The effects of the boundary layer on lift are contained in the lift coefficient and the effects on drag are contained in the drag coefficient.
Historical Note
The theory which describes boundary layer effects was first presented by Ludwig Prandtl in the early 1900’s. The general fluids equations had been known for many years, but solutions to the equations did not properly describe observed flow effects (like wing stalls). Prandtl was the first to realize that the relative magnitude of the inertial and viscous forces changed from a layer very near the surface to a region far from the surface. He first proposed the interactively coupled, two-layer solution which properly models many flow problems.