Work Done by a Gas
What is Work Done by a Gas?
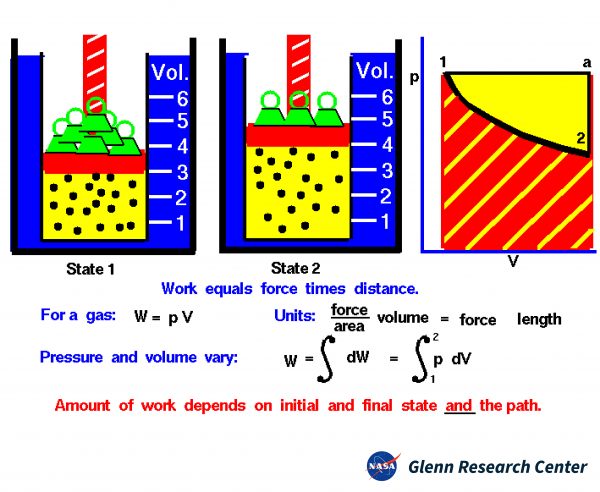
The state of a gas is determined by the values of certain measurable properties like the pressure, temperature, and volume which the gas occupies. The values of these variables and the state of the gas can be changed. On the figure we show a gas confined in a blue jar in two different states. On the left, in State 1, the gas is at a higher pressure and occupies a smaller volume than in State 2, at the right. We can represent the state of the gas on a graph of pressure versus volume, which is called a p-V diagram as shown at the right.
To change the state of the gas from State 1 to State 2, we must change the conditions in the jar, either by heating the gas, or physically changing the volume by moving a piston, or by changing the pressure by adding or removing weights from the piston. In some of these changes we do work on or have work done by the gas. In other changes we add or remove heat.
Thermodynamics helps us determine the amount of work and the amount of heat necessary to change the state of the gas. Notice that in this example we have a fixed mass of gas. We can therefore plot either the physical volume or the specific volume (volume divided by mass) since the change is the same for a constant mass. On the figure, we use physical volume.
Equations
Scientists define work W to be the product of force F acting through a distance s:
\(\LARGE W=Fs\)
For a gas, work is the product of the pressure p and the volume V during a change of volume.
\(\LARGE W=pV\)
We can do a quick units check to see that pressure force / area times volume area * length gives units of force times length which are the units of work:
\(\LARGE W=\frac{\text{force}}{\text{area}}\times\frac{\text{area}}{\text{length}}=\text{force}\times\text{length}\)
In the metric system the unit of work is the Joule, in the English system the unit is the foot-pound. In general, during a change of state both the volume and the pressure change. So, it is more correct to define the work as the integrated or summed variable pressure times the change of volume from State 1 to State 2. If we use the symbol \(\int[\>\>]\text{d}s\) for integral, then:
\(\LARGE W=\int[p]\text{d}v\)
On a graph of pressure versus volume, the work is the area under the curve that describes how the state is changed from State 1 to State 2.
Graph Explanation
As mentioned above, there are several options for changing the state of a gas from one state to another. So, we might expect that the amount of work done on, or by a gas could be different depending on exactly how the state is changed. As an example, on the graph on the figure, we show a curved black line from State 1 to State 2 of our confined gas.
This line represents a change brought about by removing weights and decreasing the pressure and allowing the volume to adjust according to Boyle’s law with no heat addition. The line is curved, and the amount of work done on the gas is shown by the red shaded area below this curve. We could, however, move from State 1 to State 2 by holding the pressure constant and increasing the volume by heating the gas using Charles’ law.
The resulting change in state proceeds from State 1 to an intermediate State “a” on the graph. State “a” is at the same pressure as State 1, but at a different volume. If we then remove the weights, holding a constant volume, we proceed on to State 2. The work done in this process is shown by the yellow shaded area. Using either process we change the state of the gas from State 1 to State 2. But the work for the constant pressure process is greater than the work for the curved line process. The work done by a gas not only depends on the initial and final states of the gas but also on the process used to change the state. Different processes can produce the same state but produce different amounts of work.
Notice that not only does the work done by the gas depend on the process, but also the heat transferred to the gas. In the first process, the curved line from State 1 to State2, no heat was transferred to the gas; the process was adiabatic. But in the second process, the straight line from State 1 to State “a” and then to State 2, heat was transferred to the gas during the constant pressure process. The heat transferred to a gas not only depends on the initial and final states of the gas but also on the process used to change the state.
