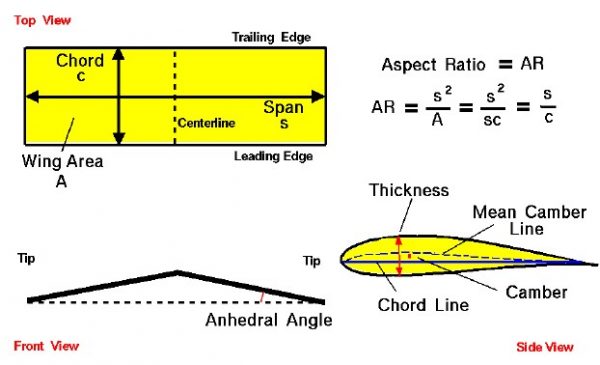
Wing Geometry
This slide gives technical definitions of a wing’s geometry, which is one of the chief factors affecting airplane lift and drag. The terminology used here is used throughout the airplane industry today and was mostly known to the Wright brothers in 1900. Actual aircraft wings are complex three-dimensional objects, but we will start with some simple definitions. The figure shows a wing viewed from three directions; the upper left shows the view from the top looking down on the wing, the lower left shows the view from the front looking at the wing leading edge, and the right shows a side view from the left looking in towards the centerline. The side view shows an airfoil shape with the leading edge to the left. This airfoil is a modern, thick airfoil, which is slightly different from the thin airfoils used by the Wrights and shown below. The terminology, however, is the same.
Top View
The top view shows a simple rectangular wing geometry, like that used by the Wright brothers. The front of the wing (at the bottom) is called the leading edge; the back of the wing (at the top) is called the trailing edge. The distance from the leading to trailing edges is called the chord. The ends of the wing are called the wing tips, and the distance from one wing tip to the other is called the span. The shape of the wing, when viewed from above looking down onto the wing, is called a planform. For a rectangular wing, the chord length at every location along the span is the same. For most modern aircraft, the chord length varies along the span, and the leading and trailing edges may be swept. The wing area is the projected area of the planform and is bounded by the leading and trailing edges and the wing tips. Note: The wing area is NOT the total surface area of the wing. The total surface area includes both upper and lower surfaces. The wing area is a projected area and is almost half of the total surface area.
The aspect ratio (AR) of a wing is defined to be the square of the span (s) divided by the wing area (A). Aspect ratio is a measure of how long and slender a wing is from tip to tip. For a rectangular wing, this reduces to the ratio of the span to the chord length (c):
AR = s^2 / A = s^2 / (s * c) = s / c
High aspect ratio wings have long spans (like high performance gliders), while low aspect ratio wings have either short spans or thick chords (like the Space Shuttle). Gliders have a high aspect ratio because the drag of the aircraft depends on this parameter. A higher aspect ratio gives a lower drag, a higher lift to drag ratio, and a better glide angle.
Front View
The front view of this wing shows that the left and right wing do not lie in the same plane but meet at an angle. The angle that the wing makes with the local horizontal is called the dihedral angle (if the tips are higher than the root) or the anhedral angle (if the tips are lower than the root). Dihedral is added to the wings for roll stability; a wing with some dihedral will naturally return to its original position if it encounters a slight roll displacement. You may have noticed that most large airliner wings are designed with dihedral. The wing tips are farther off the ground than the wing root. Highly maneuverable fighter planes, on the other hand usually have the wing tips lower than the roots giving the aircraft a high roll rate. The Wright brothers designed their 1903 flyer with a slight anhedral to improve the aircraft roll performance.
Airfoil Geometry
A cut through the wing perpendicular to the leading and trailing edges will show the cross-section of the wing. This cross-section is called an airfoil, and it has some geometry definitions of its own as shown at the lower right. The straight line drawn from the leading to trailing edges of the airfoil is called the chord line. The chord line cuts the airfoil into an upper surface and a lower surface. If we plot the points that lie halfway between the upper and lower surfaces, we obtain a curve called the mean camber line. For a symmetric airfoil the upper surface is a reflection of the lower surface and the mean camber line will fall on top of the chord line. But in most cases, the mean camber line and the chord line are two separate lines. The maximum distance between the two lines is called the camber, which is a measure of the curvature of the airfoil (high camber means high curvature). The maximum distance between the upper and lower surfaces is called the thickness. Often you will see these values divided by the chord length to produce a non-dimensional or “percent” type of number. Airfoils can come with all kinds of combinations of camber and thickness distributions.
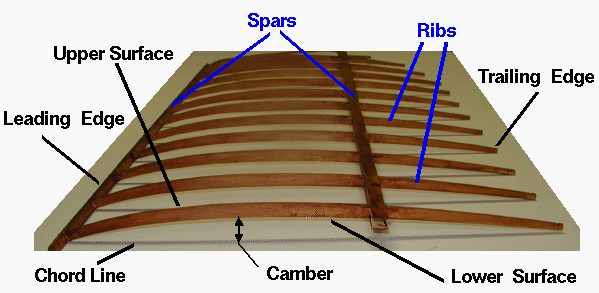
The view is looking out towards the right wing tip and the cloth skin has been removed from the wing so that the construction can be viewed. The spars are long, heavy pieces that run from wing tip to wing tip along the leading edge and near the middle of the wing. The ribs are attached to the spars and the ribs produce the airfoil shape. The Wrights developed the final geometry for their wings by testing small models in their wind tunnel in 1901. They used mechanical balances to measure the lift and drag for their wing models. The resulting airfoils were very thin, with a slight camber. Both the upper and lower surfaces were curved.
NOTICE: The upper and lower surfaces of the Wright airfoils are nearly the same length; the lower surface is not flat like many modern low speed airfoils. This is a perfect example which shows that the popular theory of lift generation found in many textbooks is completely wrong! The upper surface doesn’t have to be longer than the lower surface to generate lift. The lift occurs because the airfoil turns the flow of air and both the lower and upper surface contribute to the turning.