Weight Equation
Weight is the force generated by the gravitational attraction of the earth on any object. Weight is fundamentally different from the aerodynamic forces, lift and drag. Aerodynamic forces are mechanical forces and the object has to be in physical contact with the air which generates the force. The gravitational force is a field force; the source of the force does not have to be in physical contact with the object to generate a force.
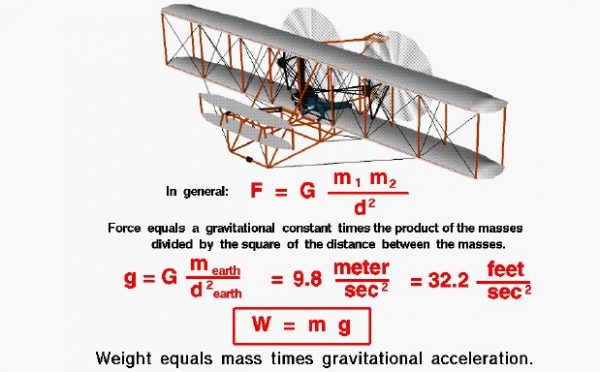
The nature of the gravitational force has been studied by scientists for many years and is still being investigated by theoretical physicists. For an object the size of an airplane flying near the earth, the descriptions given three hundred years ago by Sir Isaac Newton work quite well. Newton published his theory of gravitation with his laws of motion in 1686. The gravitational force, F, between two particles equals a universal constant, G, times the product of the mass of the particles, m1 and m2, divided by the square of the distance, d, between the particles.
F = G * m1 * m2 / d^2
If you have a lot of particles acting on a single particle, you have to add up the contribution of all the individual particles. For objects near the earth, the sum of the mass of all the particles is simply the mass of the earth and the distance is then measured from the center of the earth. On the surface of the earth the distance is about 4000 miles. Scientists have combined the universal gravitational constant, the mass of the earth, and the square of the radius of the earth to form the gravitational acceleration, g . On the surface of the earth, its value is 9.8 meters per square second or 32.2 feet per square second.
g = G * m earth / (d earth)^2
The weight W, or gravitational force, is then just the mass of an object times the gravitational acceleration.
W = m * g
Since the gravitational constant (g) depends on the square of the distance from the center of the earth, we would expect that the weight of an object would decrease with altitude. Let’s do a test problem to see how much the weight changes. If an airplane is flying at 35000 feet (about 7 miles) the distance to the center of the earth is about 4007 miles. We can calculate the change in the gravitational constant as the square of (4000/4007) which equals .9965. If the airplane weighs 10000 pounds on the surface of the earth, it weighs 9965 pounds at 35000 feet; it has lost 35 pounds, a very small amount compared to 10000 pounds.