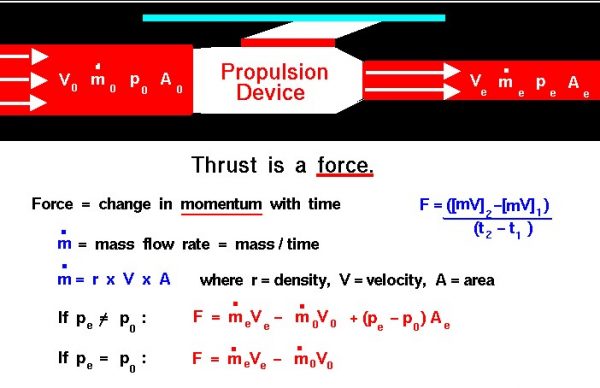
Thrust Equation
Thrust
Thrust is the force which moves an aircraft through the air. Thrust is generated by the propulsion system of the airplane.
How is thrust generated?
Thrust is a mechanical force which is generated through the reaction of accelerating a mass of gas, as explained by Newton’s third law of motion. A gas or working fluid is accelerated to the rear and the engine and aircraft are accelerated in the opposite direction. To accelerate the gas, we need some kind of propulsion system. We will discuss the details of various propulsion systems on some other pages. For right now, let us just think of the propulsion system as some machine which accelerates a gas.
Momentum
From Newton’s second law of motion, we can define a force F to be the change in momentum of an object with a change in time. Momentum is the object’s mass m times the velocity V. So, between two times t1 and t2, the force is given by:
F = ((m * V)2 – (m * V)1) / (t2 – t1)
Force
If we keep the mass constant and just change the velocity with time we obtain the simple force equation – force equals mass time acceleration a
F = m * a
Mass Flow Rate
If we are dealing with a solid, keeping track of the mass is relatively easy; the molecules of a solid are closely bound to each other and a solid retains its shape. But if we are dealing with a fluid (liquid or gas) and particularly if we are dealing with a moving fluid, keeping track of the mass gets tricky. For a moving fluid, the important parameter is the mass flow rate. Mass flow rate is the amount of mass moving through a given plane over some amount of time. Its dimensions are mass/time (kg/sec, slug/sec, …) and it is equal to the density r times the velocity V times the area A. Aerodynamicists denote this parameter as m dot (m with a little dot over the top).
m dot = r * V * A
Note: The “dot” notation is used a lot by mathematicians, scientists, and engineers as a symbol for “d/dt”, which means the variable changes with a change in time. For example, we can write Newton’s second law as either
F = d(mv)/dt or F = (mv)dot
So “m dot” is not simply the mass of the fluid, but is the mass flow rate, the mass per unit time.
Since the mass flow rate already contains the time dependence (mass/time), we can express the change in momentum across the propulsion device as the change in the mass flow rate times the velocity. We will denote the exit of the device as station “e” and the free stream as station “0”. Then
F = (m dot * V)e – (m dot * V)0
A units check shows that on the right hand side of the equation:
mass/time * length/time = mass * length / time^2
Pressure
This is the dimension of a force. There is an additional effect which we must account for if the exit pressure p is different from the free stream pressure. The fluid pressure is related to the momentum of the gas molecules and acts perpendicular to any boundary which we impose. If there is a net change of pressure in the flow there is an additional change in momentum. Across the exit area we may encounter an additional force term equal to the exit area Ae times the exit pressure minus the free stream pressure. The general thrust equation is then given by:
General Thrust Equation
F = (m dot * V)e – (m dot * V)0 + (pe – p0) * Ae
Normally, the magnitude of the pressure-area term is small relative to the m dot-V terms. Let us look at this equation very carefully, for it has some interesting implications.
Design Theory of Engines
We see that there are two possible ways to produce high thrust. One way is to make the engine flow rate (m dot) as high as possible. As long as the exit velocity is greater than the free stream, entrance velocity, a high engine flow will produce high thrust. This is the design theory behind propeller aircraft and high-bypass turbofan engines. A large amount of air is processed each second, but the velocity is not changed very much. The other way to produce high thrust is to make the exit velocity very much greater than the incoming velocity. This is the design theory behind pure turbojets, turbojets with afterburners, and rockets. A moderate amount of flow is accelerated to a high velocity in these engines. If the exit velocity becomes very high, there are other physical processes which become important and affect the efficiency of the engine. These effects are described in detail on other pages at this site.
Gas Turbine Engine
There is a simplified version of the general thrust equation that can be used for gas turbine engines. The nozzle of a turbine engine is usually designed to make the exit pressure equal to free stream. In that case, the pressure-area term in the general equation is equal to zero. The thrust is then equal to the exit mass flow rate times the exit velocity minus the free stream mass flow rate times the free stream velocity.
F = (m dot * V)e – (m dot * V)0
The first term on the right hand side of this equation is usually called the gross thrust of the engine, while the second term is called the ram drag. It is a drag term because it is subtracted from the gross thrust.
Since the exit mass flow rate is nearly equal to the free stream mass flow rate, and the free stream is all air, we can call the mass flow rate through the engine the engine airflow rate.
F = (m dot)eng * (Ve – V0)
We can further simplify by absorbing the engine airflow dependence into a more useful parameter called the specific thrust Fs. Specific thrust only depends on the velocity change across the engine.
Fs = F /(m dot)eng = (Ve – V0)
General Thrust Equation for Rocket Engines
There is a different simplified version of the general thrust equation that can be used for rocket engines. Since a rocket carries its own oxygen on board, there is no ram drag for a rocket engine. The general equation simplifies to:
F = (m dot * V)e + (pe – p0) * Ae
We have to include the pressure correction term since a rocket nozzle produces a fixed exit pressure which in general is different than free stream pressure. There is a useful rocket performance parameter called the specific impulse Isp, that eliminates the mass flow dependence in the analysis.
Isp = Veq / go
where Veq is the equivalent velocity, which is equal to the nozzle exit velocity plus the pressure-area term, and g0 is the gravitational acceleration.
Nozzle
For both rockets and turbojets, the nozzle performs two important roles. The design of the nozzle determines the exit velocity for a given pressure and temperature. And because of flow choking in the throat of the nozzle, the nozzle design also sets the mass flow rate through the propulsion system. Therefore, the nozzle design determines the thrust of the propulsion system as defined on this page. You can investigate nozzle operation with our interactive thrust simulator.