Rocket Translation
Dimensions
We live in world that is defined by three spatial dimensions and one time dimension. Objects can move within this domain in two ways. An object can translate, or change location, from one point to another. And an object can rotate or change its attitude. In general, the motion of an object involves both translation and rotation. The motion of a rocket is particularly complex because the rotations and translations are coupled together; a rotation affects the magnitude and direction of the forces which affect translations.
Translation of Rockets
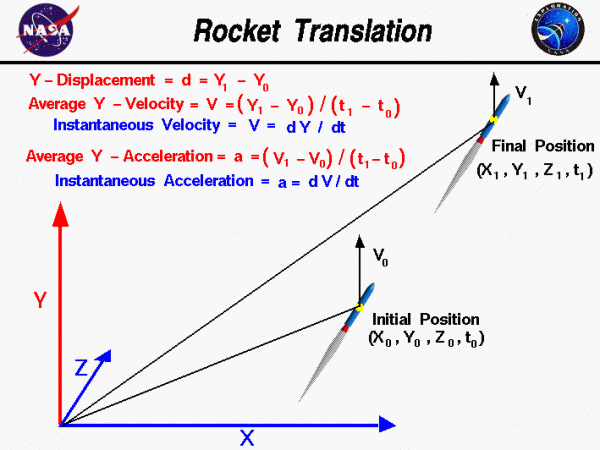
On this page we will consider only the translation of a rocket within our domain. We can specify the location of our rocket at any time t by specifying three coordinates x, y, and z on an orthogonal coordinate system. An orthogonal coordinate system has each of its coordinate directions perpendicular to all other coordinate directions. Initially, our rocket is at point “0”, with coordinates x0, y0, and z0 at time t0. In general, the rocket moves through the domain until at some later time t1 the rocket is at point “1” with coordinates x1, y1, and z1. We can specify the displacement – d in each coordinate direction by the difference in coordinate from point “0” to point “1”. The x-displacement equals (x1 – x0), the y-displacement equals (y1 – y0), and the z-displacement equals (z1 – z0). On this page we only present displacement in the y-coordinate to help the student better understand the fundamentals of motion.
\(\LARGE d=y_{1}-y_{0}\)
The total displacement is a vector quantity with the x-, y-, and z-displacements being the components of the displacement vector in the coordinate directions. All of the quantities derived from the displacement are also vector quantities.
Velocity of the Rockets
The velocity -V of the rocket through the domain is the derivative of the displacement with respect to time. In the Y – direction, the average velocity is the displacement divided by the time interval:
\(\LARGE V=\frac{y_{1}-y_{0}}{t_{1}-t_{0}}\)
This is only an average velocity; the rocket could speed up and slow down inside the domain. At any instant, the rocket could have a velocity that is different than the average. If we shrink the time difference down to a very small (differential) size, we can define the instantaneous velocity to be the differential change in position divided by the differential change in time:
\(\LARGE V=\frac{\text{d}Y}{\text{d}t}\)
where the symbol d / dt is the differential from calculus. So when we initially specified the location of our aircraft with x0, y0, z0, and t0 coordinates, we could also specify an initial instantaneous velocity V0. Likewise at the final position x1, y1, z1, and t1, the velocity could change to some V1. We are here considering only the y-component of the velocity. In reality, the rocket velocity changes in all three directions. Velocity is a vector quantity; it has both a magnitude and a direction.
Acceleration of the Rockets
The acceleration (a) of the rocket through the domain is the derivative of the velocity with respect to time. In the Y – direction, the average acceleration is the change in velocity divided by the time interval:
\(\LARGE a=\frac{V_{1}-V_{0}}{t_{1}-t_{0}}\)
As with the velocity, this is only an average. At any instant, the rocket could have an acceleration that is different than the average. If we shrink the time difference down to a very small (differential) size, we can define the instantaneous acceleration to be the differential change in velocity divided by the differential change in time:
\(\LARGE a=\frac{\text{d}V}{\text{d}t}\)
From Newton’s second law of motion, we know that forces on an object produce accelerations. If we can determine the forces on a rocket, and how they change, we can use the equations presented on this slide to determine the location and velocity of the rocket as a function of the time.