Rocket Center of Pressure

As a model rocket flies through the air, aerodynamic forces act on all parts of the rocket. In the same way that the weight of all the rocket components acts through the center of gravity cg, the aerodynamic forces act through a single point called the center of pressure cp. How do you determine the location of the center of pressure?

Determining the Location of the Center of Pressure

You can calculate the center of pressure. But, in general, this is a complicated procedure requiring the use of calculus. The aerodynamic forces are the result of pressure variations around the surface of the rocket. In general, you must determine the integral of the pressure times the unit normal, times the area, times the distance from a reference line. Then divide by the integral of the pressure times the unit normal, times the area. Lots of work! For a model rocket, there are some simplifying assumptions that we can use to make this task much easier.

Model rockets are fairly symmetric about the axis of the rocket. This allows us to reduce the full three-dimensional problem to a simple, two-dimensional cut through the axis of the rocket. For model rockets, the magnitude of the pressure variation is quite small. If we assume that the pressure is nearly constant, finding the average location of the pressure times the area distribution reduces to finding just the average location of the projected area distribution.

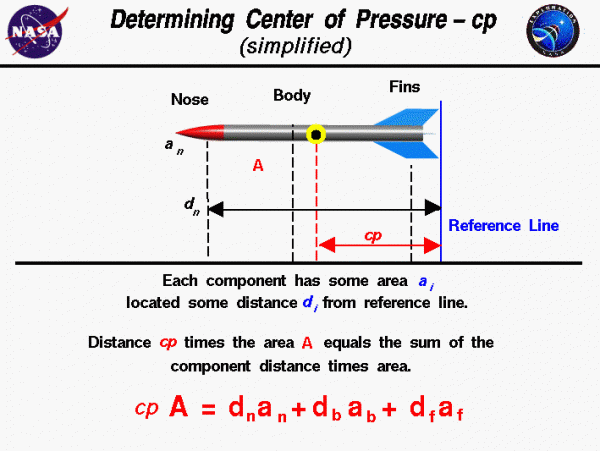
Simplified Calculation of cp

The figure shows a simplified version of the calculation procedure that you can use to calculate the cp of a model rocket. We assume that we already know the projected area and location, relative to some reference location, of each of the major parts of the rocket: the nose, body tube, and fins. The projected area A of the rocket is the sum of the projected area a of the components.

\(\LARGE A=a(\text{nose})+a(\text{tube})+a(\text{fins})\)

Since the center of pressure is an average location of the projected area, we can say that the area of the whole rocket times the location of the center of pressure cp is equal to the sum of the projected area of each component times the distance d of that component from the reference location.

\(\LARGE A\cdot\mathit{cp}=[ad](\text{nose})+[ad](\text{tube})+[ad](\text{fins})\)

The “location” of each component is the distance of each component’s center of pressure from the reference line. So, you must calculate or determine the center of pressure of each of the components. For example, the projected area of the body tube is a rectangle. The center of pressure is on the axis, halfway between the end planes.

Mechanically determining cp

For a model rocket, there is a simple mechanical way to determine the center of pressure for each component or for the entire rocket. Make a two-dimensional tracing of the shape of the component, or rocket, on a piece of cardboard and cut out the shape. Hang the cut-out shape by a string and determine the point at which it balances. This is just like balancing a pencil with a string! The point at which the component, or rocket, is balanced is the center of pressure. You obviously could not use this procedure for a very large rocket like the Space Shuttle. But it works quite well for a model.