Rocket Center of Gravity

Rocket’s Essential Factors

As a rocket flies through the air, it both translates and rotates. The rotation occurs about a point called the center of gravity. The center of gravity is the average location of the weight of the rocket. The mass and weight are distributed throughout the rocket, and for some problems, it is important to know the distribution. But for rocket trajectory and maneuvering, we need to be concerned with only the total weight and the location of the center of gravity.

Determining the Location of the Center of Gravity

Calculating cg

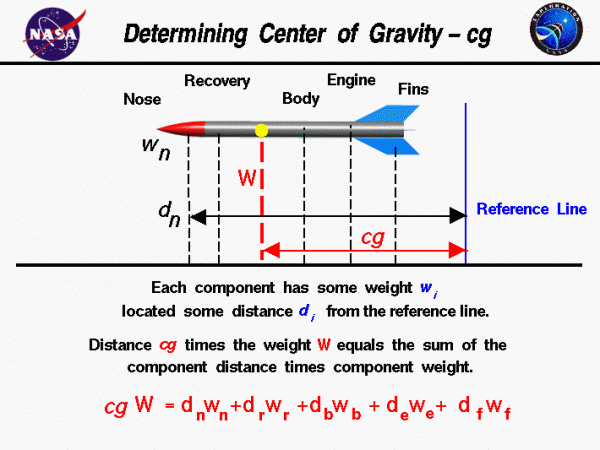
A model rocket is a combination of many parts: the nose cone, payload, recovery system, body tube, engine, and fins. Each part has a weight associated with it which you can estimate, or calculate, using Newton’s weight equation:

\(\LARGE w=mg\)

where w is the weight, m is the mass, and g is the gravitational constant which is 32.2 ft/square sec in English units and 9.8 meters/square sec in metric units on the surface of the Earth. On the Moon and Mars, the gravitational constant and the resulting weight is less than on Earth. To determine the center of gravity c_g, we choose a reference location, or reference line. The cg is determined relative to this reference location. The total weight of the model rocket is simply the sum of all the individual weights of the components. Since the center of gravity is an average location of the weight, we can say that the weight of the rocket W times the location cg of the center of gravity is equal to the sum of the weight w of each component times the distance d of that component from the reference location:

\(\LARGE W\cdot\mathit{cg}=[wd](\text{nose})+[wd](\text{recovery})+[wd](\text{engine})+\text{…}\)

The center of gravity is the mass-weighted average of the component locations.

Determining cg Mechanically

For a small model rocket, there is a simple mechanical way to determine the c_g for each component or for the entire rocket:

1. For simple geometries we just balance the component or the entire rocket using a string or an edge. The point at which the component or rocket is balanced is the center of gravity. This is just like balancing a pencil on your finger! Obviously, we could not use this procedure for a large rocket like the Space Shuttle, but it works quite well for a model.
2. Another, more complicated way, is to hang the model from some point, for example, the corner of a fin, and drop a weighted string from the same point. Draw a line on the rocket along the string. Repeat the procedure from another point on the rocket, the nose, for example. You now have two lines drawn on the rocket. The c_g is the point where the lines intersect. This procedure works well for irregularly shaped objects that are hard to balance. The problem with this procedure is that the cg can fall outside the body for complex geometries.

Components’ Location

On this page, we show the weight and distance of the nose cone from the reference line. A similar distance can be determined for each component relative to the reference line. How do we determine the distance d? Using the nose cone as an example, the “distance” of the nose d_n is the distance of the cg of the nose relative to the reference line.

So, we have to be able to calculate or determine the cg of the nose cone and each of the other rocket components. For some simple shapes, finding the cg, or average location of the weight, is quite simple. For example, when viewed perpendicular to the axis, the body tube is rectangular. The cg is on the axis, halfway between the end planes. For other shapes, like the nose cone, determining the cg of the component is not so simple. There is a technique for determining the cg of any general shape, and the details of this technique are given on another page.