Model Rocket Weight

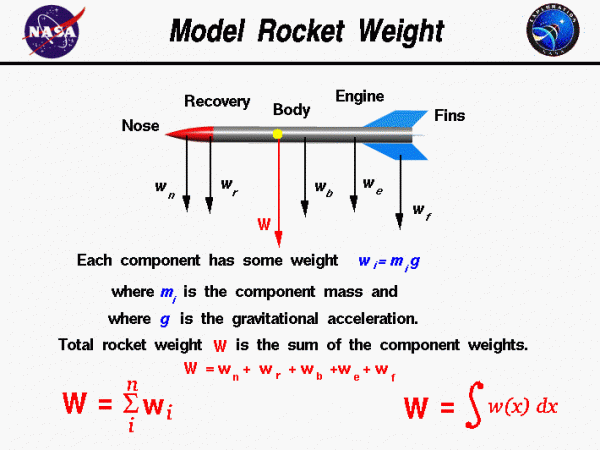
Weight

Weight is the force generated by the gravitational attraction of a planet on the mass of a rocket. Weight is related to the mass through the weight equation and each part of a rocket has a unique weight and mass. For some problems it is important to know the distribution of weight. But for rocket trajectory and stability, we only need to be concerned with the total weight and the location of the center of gravity. For model rockets and compressed air rockets the weight remains fairly constant during the flight and we can easily compute the weight of the rocket. But for water rockets and full scale rockets the weight changes during launch.

Determining the Weight of Model Rocket

A model rocket is a combination of many parts: the nose cone, payload, recovery system, frame, engine, and fins. Each part has a weight associated with it which you can determine using a scale, or calculate, using Newton’s general weight equation:

\(\LARGE w=mg\)

where w is the weight, m is the mass, and g is the gravitational constant which is 32.2 ft/square sec in English units and 9.8 meters/square sec in metric units on the surface of the Earth. On the Moon and Mars, the gravitational constant and the resulting weight is less than on Earth. The mass of any individual component can be calculated if we know the size of the component and its chemical composition. Every material (aluminum, balsa wood, plastic, rocket fuel, etc.) has a unique density. Density r is defined to be the mass divided by the volume v:

\(\LARGE r=\frac{m}{v}\)

If we can calculate the volume of the component, then:

\(\LARGE m=rv\)

The total weight W of the rocket is simply the sum of the weight of all of the individual components.

\(\LARGE W=w(\text{nose})+w(\text{recovery})+w(\text{engines})+w(\text{body})\\ \LARGE+w(\text{fins})\)

Generalization

If we have a total of “n” discrete components, the weight of the rocket is the sum of the individual i component weights with the index i going from 1 to n. The Greek letter sigma (\(\bf\sum\)) is used by mathematicians to denote this addition.

\(\LARGE W=\sum_{i}^{n}w_{i}\)

This equation says that the weight of the rocket is equal to the sum of the weight of “n” discrete parts.

What if the parts are not discrete?

What if we had a continuous change of mass from front to back, as occurs with a solid balsa nose cone? The continuous change can be computed using integral calculus. The sigma designation is changed to the integral “\(\int\)” shaped symbol to denote a continuous variation.

\(\LARGE W=\int w(x){\text{d}x}\)

The discrete weight is replaced with w(x) which indicates that the weight is some function of distance x. If we are given the form of the function, there are methods to solve the integration. If we don’t know the actual functional form, we can still numerically integrate the equation using a spread sheet by dividing the distance up into a number of small distance segments and determining the average value of the weight over that small segment, then summing up the value.