Mars Atmosphere Equation – Metric

Atmosphere of Mars

The Martian atmosphere is an extremely thin sheet of gas, principally carbon dioxide, that extends from the surface of Mars to the edge of space. The Martian atmosphere is less dense than the Earth’s atmosphere, but there are many similarities. Gravity holds the atmosphere to the Martian surface. Within the atmosphere, very complex chemical, thermodynamic, and fluid dynamics effects occur. The atmosphere is not uniform; fluid properties are constantly changing with time and place producing weather on Mars just like on Earth.

Variation in Atmospheric Properties

Variations in atmospheric properties extend upward from the surface of Mars. The sun heats the surface, and some of this heat goes into warming the gas near the surface. The heated gas is then diffused or convected up through the atmosphere. Thus, the gas temperature is highest near the surface and decreases as altitude increases. The speed of sound depends on the temperature and also decreases with increasing altitude. As with the Earth, the pressure in the atmosphere decreases with altitude. The density of the atmosphere depends on both the temperature and the pressure through the equation of state and also decreases with increasing altitude.

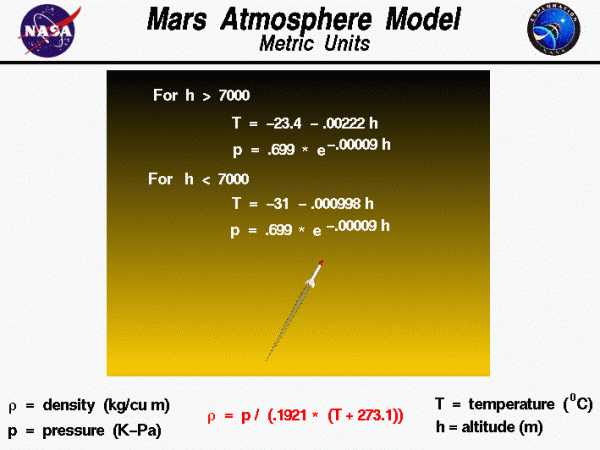
Mathematical Model of the Atmosphere

Aerodynamic forces directly depend on the gas density. To help spacecraft designers, it is useful to define a mathematical model of the atmosphere to capture the effects of altitude. The model shown here was developed from measurements of the Martian atmosphere made by the Mars Global Surveyor in April 1996. The information on the Martian atmosphere was gathered by Jonathon Donadee of Canfield (Ohio) Middle School during a cyber-mentoring program in 1999. The data was curve fit to produce equations by Dave Hiltner of St. John’s Jesuit High School as part of a shadowing program in May 1999. The curve fits are given for Metric units. These curve fits are also available in English units.

Two Zones of the Model

The model has two zones with separate curve fits for the lower atmosphere and the upper atmosphere. The lower atmosphere runs from the surface of Mars to 7,000 meters. In the lower atmosphere, the temperature decreases linearly, and the pressure decreases exponentially. The rate of temperature decrease is called the lapse rate. For the temperature T and the pressure p, the metric units curve fits for the lower atmosphere are:

\(\LARGE T=-31-0.000998h\)

\(\LARGE p=.699e^{-0.00009h}\)

where the temperature is given in Celsius degrees, the pressure in kilopascals, and h is the altitude in meters. The upper stratosphere model is used for altitudes above 7,000 meters. In the upper atmosphere the temperature decreases linearly, and the pressure decreases exponentially. The metric units curve fits for the upper atmosphere are:

\(\LARGE T=-23.4-0.00222h\)

\(\LARGE p=.669e^{-0.00009h}\)

In each zone the density rho (\(\rho\)) is derived from the equation of state:

\(\LARGE \rho=\frac{p}{.1921(T+273.1)}\)

Note

Comparing this equation with the similar equation of state for the Earth’s atmosphere, you will notice that the gas constants are different, .1921 for Mars and .2869 for Earth. These numbers are different because the Martian atmosphere is almost entirely composed of carbon dioxide, while the Earth’s atmosphere is a mixture of 78% nitrogen and 21% oxygen.

This is the atmosphere model used in the RocketModeler simulator. An interactive simulation for the atmosphere model is also available. With the applet, you can change altitude and see the effects on pressure and temperature.