Graphical Maximum Altitude

Flying Model Rockets

Flying model rockets is a relatively safe and inexpensive way for students to learn the basics of forces and the response of vehicles to external forces. Students can also use math techniques learned in high school to determine the performance of the rocket during the flight.

Determining the Altitude of Model Rocket

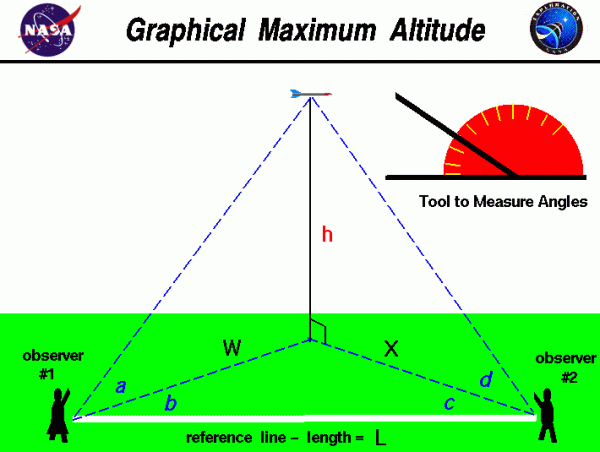
On this page we show a simple way to determine the altitude of a model rocket. The procedure requires two observers and a tool, like the one shown in the upper right portion of the figure, to measure angles. The observers are stationed some distance L along a reference line. You can lay a string of known length along the ground between the observers to make this reference line. A long line produces more accurate results.

As the rocket passes its maximum altitude, observer #1 calls out “Take Data”, and measures the angle a between the ground and the rocket. This measurement is taken perpendicular to the ground. Observer #1 then measures the angle b between the rocket and the reference line. This measurement is taken parallel to the ground and can be done by the observer facing the rocket, holding position, and measuring from the direction the observer is facing to the reference line on the ground.

When the second observer hears the call, “Take Data”, the observer must face the rocket and measure the angle d from the ground to the rocket. The second observer must then measure the angle c, parallel to the ground, between the direction the observer is facing and the reference line in the same manner as the first observer. Angles a and d are measured in a plane that is perpendicular to the ground while angles b and c are measured in a plane parallel to the ground.

Building Scale Model of the Rocket

With the four measured angles and the measured distance between the observers, we can use graph paper to build a scale model of the rocket in flight and we can determine the altitude h of the actual rocket. Scale models depend on the mathematical ideas of ratios and proportions which you learn in grade school.

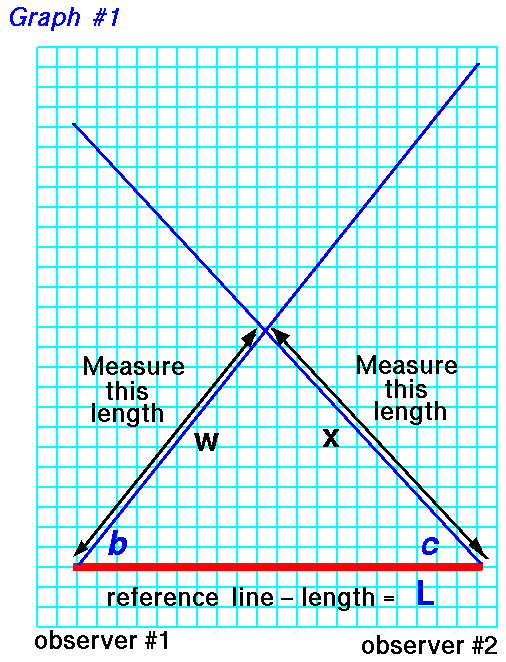
To determine the altitude, we first draw the reference line L on the graph paper. Make the length of the line on the graph paper some known ratio of the measured length. The length of the line on the graph paper sets the scale of the model. For instance, if the measured length was 100 feet, we might make the line on the graph paper 10 inches long. Then one inch on the graph paper equals 10 feet in the real world.

Now draw two lines beginning at the ends of the reference line and inclined at the measured angles b and c.

Measuring Distance

On the graph paper use a ruler to measure the distance w from the beginning of the reference line, near observer #1, to the intersection of the two drawn lines. The intersection point marks the location on the ground that is directly beneath the flying rocket. Also measure the distance x from the end of reference line, near observer #2.

Measuring Altitude

As discussed on the web page with the derivation of the equations, we really only need three measured angles and the reference length to accurately determine the altitude. So you can use either angle a measured by observer #1, or angle d measured by observer #2, to determine the altitude. If you measure all four angles, you can make two estimates of the altitude h; they should be the same answer, but if they aren’t, you can average them.

Deriving Graph # 2

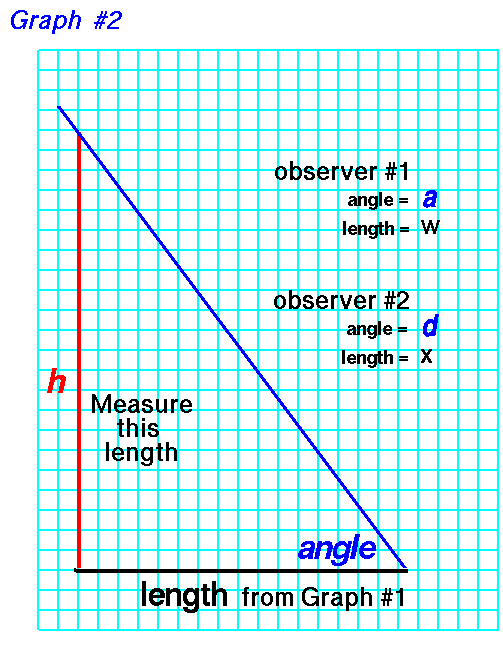
For the measurements of observer #1, on another piece of graph paper, draw a line of length w which you measured on the previous piece of graph paper. At one end of this line, draw another line inclined at the angle a. On the other end of the w line, draw a vertical line until it intersects the blue line inclined at angle a.

Measuring the Length

Now count the blocks, or measure the length, of the vertical line h. Convert this distance by the scale of the reference line, and you have determined the altitude h of the actual rocket. If you use the measurements of observer #2, substitute the length x for length w and angle d for angle a. For instance, in our example, 1-inch equals 10 feet. If your measured height h is 10 inches, the actual rocket was flying 100 feet in the air. If you understand the mathematical ideas of trigonometry, you can also calculate the altitude of model rocket and check your graphical solution.