Glider Trajectory Problem

Glider

A glider is a special kind of aircraft that has no engine. Paper airplanes are the most obvious example, but gliders come in a wide range of sizes. Toy gliders, made of balsa wood or Styrofoam, are an excellent way for students to study the basics of aerodynamics. Hang-gliders are piloted aircraft that are launched by leaping off the side of a hill. The Wright brothers perfected the design of the first airplane and gained piloting experience through a series of glider flights from 1900 to 1903.More sophisticated gliders are launched by ground based catapults, or are towed aloft by a powered aircraft then cut free to glide for hours over many miles.

Glide Angle

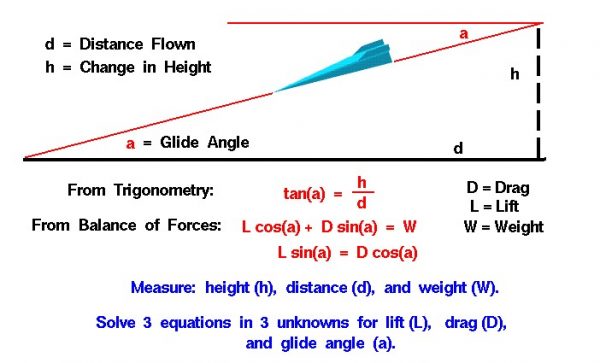
If a glider is in a steady (constant velocity and no acceleration) descent, it loses altitude as it travels. The glider’s flight path is a simple straight line, shown as the inclined red line in the figure. The flight path intersects the ground at an angle a called the glide angle. If we know the distance flown and the altitude change, we can calculate the glide angle using trigonometry. The tangent tan of the glide angle a is equal to the change in height h divided by the distance flown d:

tan(a) = h / d

Vector Components

Considering the balance of forces for a glider, we get two vector component equations. The lift L times the cosine cos of the glide angle plus the drag D times the sine sin of the glide angle is equal to the weight W:

L * cos(a) + D * sin(a) = W

The lift times the sine of the glide angle is equal to the drag times the cosine of the glide angle.

L * sin(a) = D * cos(a)

Lift and Drag of a Glider

With these three equations we can experimentally determine the lift and drag of a glider. If we test fly the glider and measure the distance along the ground, the height at which the glider is released, we can use the first equation to give us an average value of the glide angle. With the glide angle known and a measurement of the weight, we have two remaining equations in two unknowns which can be solved for the lift and the drag.