Flight To Orbit
Study Of Rockets
The study of rockets is an excellent way for students to learn the basics of forces and the response of an object to external forces. All rockets use the thrust generated by a propulsion system to overcome the weight of the rocket. The aerodynamic drag and lift are important forces acting on the toy rockets, like stomp rockets, bottle rockets, and model rockets. For air-to-air and ground-to-air missiles, the aerodynamic forces are also significant. Aerodynamic forces are not as important for satellite launchers, because of the flight trajectory to orbit. The rocket gets out of the atmosphere as quickly as possible, then gains the velocity needed to remain in orbit.
Thrust and Weight
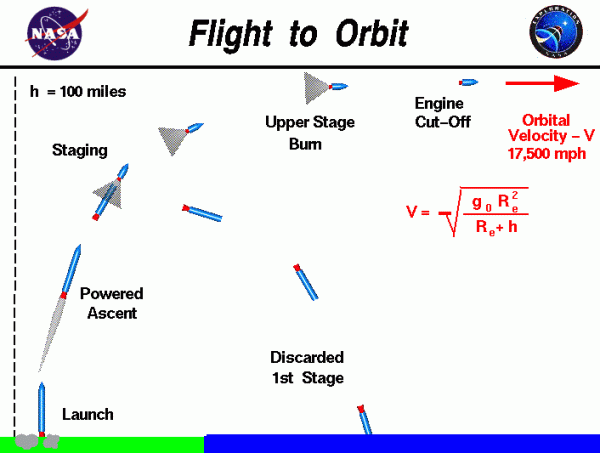
On this page we show the major events in the flight of a two-stage launch to orbit. Throughout the flight, the weight of the rocket is constantly changing because of the burning of the propellants. At launch, the thrust produced by the engine is greater than the weight of the rocket and the net force accelerates the rocket away from the pad. Unlike model rockets, full scale launchers rely on a sophisticated guidance system to balance and steer the rocket during its flight. The thrust of the rocket is gimbaled, or rotated, during the flight to produce maneuvers. Leaving the pad, the rocket begins a powered vertical ascent. The vehicle accelerates because of the high thrust and decreasing weight and rather quickly moves out of the thick atmosphere near the surface of the earth. Although the rocket is traveling supersonically, the drag on the vehicle is small because of the shape of the rocket and the lower air density at altitude. As the rocket ascends, it also begins to pitch over, and its flight path becomes more inclined to the vertical.
Staging
Several minutes into the ascent, most launchers discard some of the weight of the rocket. This process is called staging and often includes the ignition of a second engine, or upper stage, of the launcher. The discarded first stage continues on a ballistic flight back to Earth. The first stage may be retrieved, as with the Space Shuttle solid rocket engines, or it may be completely discarded, as was done on the Apollo moon rockets.
The lighter, upper stage continues to accelerate under the power of its engine and to pitch over to the horizontal. At a carefully determined altitude and speed, the upper stage engine is cut off and the stage and payload are in orbit. The exact speed needed to orbit the earth depends on the altitude, according to a formula that was developed by Johannes Kepler in the early 1600’s:
\(\LARGE V=\sqrt{\frac{g_{0}R_{e}^{2}}{R_{e}+h}}\)
where V is the velocity for a circular orbit, g0 is the surface gravitational constant of the Earth (32.2 ft/sec2), Re is the mean Earth radius (3963 miles), and h is the height of the orbit in miles. If the rocket was launched from the Moon or Mars, the rocket would require a different orbital velocity because of the different planetary radius and gravitational constant. For a 100-mile-high orbit around the Earth, the orbital velocity is 17,478 mph. Knowing the velocity and the radius of the circular orbit, we can also calculate the time needed to complete an orbit. This time is called the orbital period.
\(\LARGE T^{2}=\frac{4\pi^{2}(R_{e}+h)^{3}}{g_{0}R_{e}^{2}}\)
Looking at these equations, we see that as the height above the planet increases, the velocity needed to maintain an orbit decreases. A spacecraft flying at a lower orbit must travel faster than a spacecraft flying at a higher orbit.
We have developed a simulation called CircularOrbit that you can use to study the effects of altitude, velocity, and orbital period on the orbit of a satellite around any planet in the solar system.
While they cannot fly all the way to orbit, there are two stage model rocket kits available. You can study the flight characteristics of a two-stage model rocket by using the RocketModeler III simulation program.
