Falling Object with Air Resistance

Force

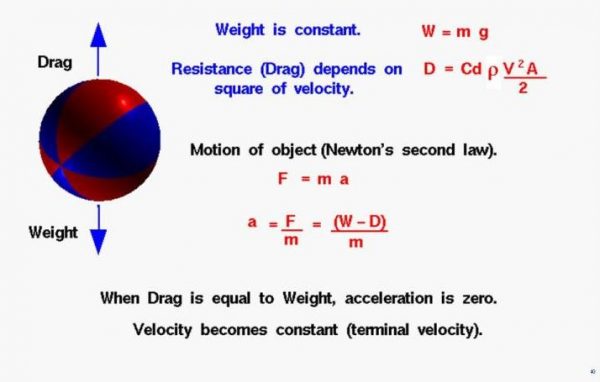
An object that is falling through the atmosphere is subjected to two external forces. The first force is the gravitational force, expressed as the weight of the object, and the second force is the aerodynamic drag of the object. The weight equation defines the weight W to be equal to the mass m of the object times the gravitational acceleration g:

W = m * g

Gravitational Acceleration

The value of g is 9.8 meters per square second on the surface of the earth. The gravitational acceleration decreases with the square of the distance from the center of the earth. But for most practical problems in the atmosphere, we can assume this factor is constant. If the object were falling in a vacuum, this would be the only force acting on the object. But in the atmosphere, the motion of a falling object is opposed by the aerodynamic drag. The drag equation tells us that drag D is equal to a drag coefficient Cd times one half the air density r times the velocity V squared times a reference area A on which the drag coefficient is based:

On the figure at the top, the density is expressed by the Greek symbol “rho”. The symbol looks like a script “p”. This is the standard symbol used by aeronautical engineers. We are using “r” in the text for ease of translation by interpretive software.

D = Cd * .5 * r * V^2 * A

Newton’s Second Law of Motion

The motion of any moving object can be described by Newton’s second law of motion, force F equals mass m times acceleration a:

F = m * a

We can do a little algebra and solve for the acceleration of the object in terms of the net external force and the mass of the object:

a = F / m

Weight and drag are forces which are vector quantities. The net external force is then equal to the difference of the weight and the drag forces:

F = W – D

The acceleration of the object then becomes:

a = (W – D) / m

Drag Force

The drag force depends on the square of the velocity. So as the body accelerates its velocity and the drag increase. It quickly reaches a point where the drag is exactly equal to the weight. When drag is equal to weight, there is no net external force on the object, and the acceleration becomes zero. The object then falls at a constant velocity as described by Newton’s first law of motion. The constant velocity is called the terminal velocity.