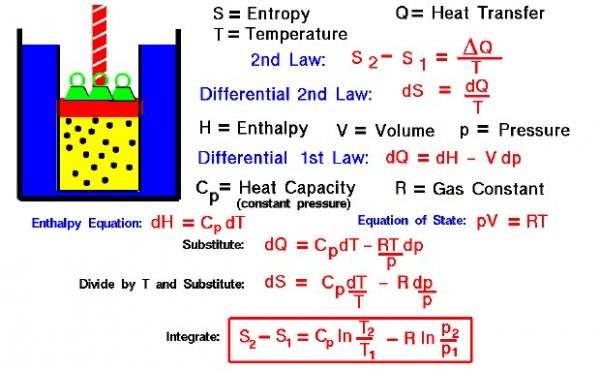
Entropy of a Gas

Thermodynamics is a branch of physics that deals with the energy and work of a system. As aerodynamicists, we are most interested in thermodynamics in the study of propulsion systems. The first law of thermodynamics indicates that the total energy of a system is conserved. This includes the potential and kinetic energy, the work done by the system, and the transfer of heat through the system. The second law of thermodynamics indicates that, while many physical processes that satisfy the first law are possible, the only processes that occur in nature are those for which the entropy (S) of the system either remains constant or increases. Entropy, like temperature (T) and pressure (p), is a state variable of the system. Entropy is defined to be the heat transfer, shown as delta (Δ) Q, into the system divided by the temperature. For a process going from state 1 to state 2:

\(\LARGE S_2-S_1=\frac{\Delta Q}T\)

During a thermodynamic process, the temperature of an object changes as heat is applied or extracted. So a more correct definition of the entropy is the differential form that accounts for this variation.

\(\LARGE dS=\frac{dQ}T\)

The change in entropy is then the inverse of the temperature integrated over the change in heat transfer. For gases, there are two possible ways to evaluate the change in entropy. The equations can be formulated in terms of the internal energy (E) and the work (W) for a gas. Or, it may be formulated in terms of the enthalpy (H) of the gas. We shall present here the enthalpy formulation because we will use the entropy relations to determine how the temperature changes for a change in pressure inside a cylinder of the Wright 1903 engine.

Let us begin by deriving a differential form of the first law of thermodynamics. The first law is given by:

\(\LARGE E_2-E_1=Q-W\)

The differential form would be:

\(\LARGE dE=dQ-dW\)

For a gas, the work is given by

\(\LARGE dW=p\cdot dV\)

Substituting:

\(\LARGE dE=dQ-p\cdot dV\)

From the definition of enthalpy:

\(\LARGE H=E+p\cdot V\)

\(\LARGE dH=dE+p\cdot dV+V\cdot dp\)

\(\LARGE dE=dH-p\cdot dV-V\cdot dp\)

Substitute into the first law equation:

\(\LARGE dH-p\cdot dV-V\cdot dp=dQ-p\cdot dV\)

\(\LARGE dH-V\cdot dp=dQ\)

Using the equation of state, we can modify the second term of this equation in terms of the gas constant, the pressure, and the temperature.

\(\LARGE p\cdot V=R\cdot T\)

\(\LARGE dH-\frac{\left(R\cdot T\right)\cdot dp}p=dQ\)

The enthalpy of a gas is equal to the specific heat of constant pressure times the change in temperature; in differential form:

\(\LARGE dH=Cp\cdot dT\)

\(\LARGE Cp\cdot dT-\frac{\left(R\cdot T\right)\cdot dp}p=dQ\)

Divide by the temperature and substitute \(dS=\frac{dQ}T\) :

\(\LARGE \frac{Cp\cdot dT}T-\frac{R\cdot dp}p=dS\)

This is a differential equations which we can easily integrate.

\(\LARGE S_2-S_1=Cp\cdot\ln\left(\frac{T_2}{T_1}\right)-R\cdot\ln\left(\frac{p_2}{p_1}\right)\)

The “ln” is the natural logarithm function which you find on your calculator and which is given in tables in math books.

What good is all of this?

There are several processes which take place within an engine for which there is no transfer of heat into the system. A simple compression is one of these adiabatic processes. If there is no heat transfer, the change of entropy is zero and we have a process that is reversible. The equation derived above relates the change in temperature to the change in pressure. For a given compression ratio, we can determine how hot the gas becomes.