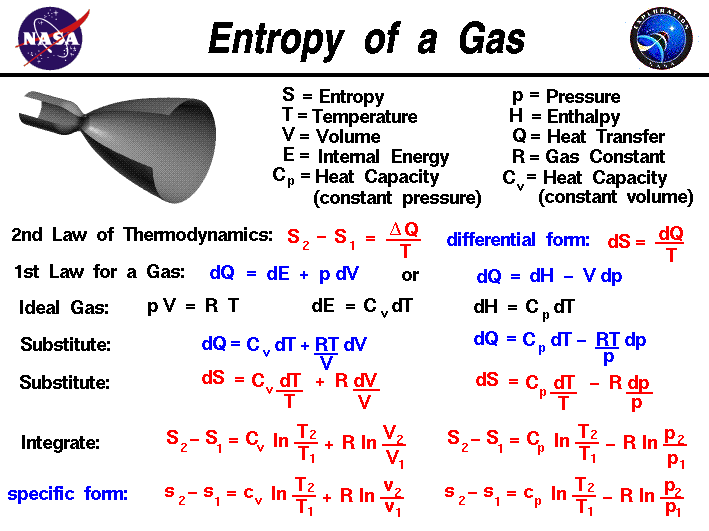Entropy of a Gas
What is Entropy?
Entropy, like temperature and pressure, can be explained on both a macro scale and a micro scale. Since thermodynamics deals only with the macro scale, the change in entropy \(\bf \Delta S\) is defined here to be the heat transfer \(\bf \Delta Q\) into the system divided by the temperature T:
\(\LARGE \Delta S=\frac{\Delta Q}{T}\)
Equations
During a thermodynamic process, the temperature T of an object changes as heat Q is applied or extracted. A more correct definition of the entropy S is the differential form that accounts for this variation.
\(\LARGE \text{d} S=\frac{\text{d} Q}{T}\)
The change in entropy is then the inverse of the temperature integrated over the change in heat transfer. For gases, there are two possible ways to evaluate the change in entropy. We begin by using the first law of thermodynamics:
\(\LARGE \text{d} E=\text{d} Q-\text{d} W\)
where E is the internal energy and W is the work done by the system. Substituting for the definition of work for a gas.
\(\LARGE \text{d}Q=\text{d}E+p\text{d}V\)
where p is the pressure and V is the volume of the gas. If we use the definition of the enthalpy H of a gas:
\(\LARGE H=E+pV\)
Then:
\(\LARGE \text{d}H=\text{d}E+p\text{d}V+V\text{d}p\)
Substitute into the first law equation:
\(\LARGE \text{d}Q=\text{d}H-V\text{d}p-p\text{d}V+p\text{d}V\)
\(\LARGE \text{d}Q=\text{d}H-V\text{d}p\)
is an alternate way to present the first law of thermodynamics. For an ideal gas, the equation of state is written:
\(\LARGE pV=RT\)
where R is the gas constant. The heat transfer of a gas is equal to the heat capacity times the change in temperature, in differential form:
\(\LARGE \text{d}Q=C\text{d}T\)
If we have a constant volume process, the formulation of the first law gives:
\(\LARGE \text{d}E=\text{d}Q=C(\text{constant volume})\text{d}T\)
Similarly, for a constant pressure process, the formulation of the first law gives:
\(\LARGE \text{d}H=\text{d}Q=C(\text{constant pressure})\text{d}T\)
If we assume that the heat capacity is constant with temperature, we can use these two equations to define the change in enthalpy and internal energy. If we substitute the value for p from the equation of state, and the definition of dE in the first energy equation, we obtain:
\(\LARGE \text{d}Q=C(\text{constant volume})\text{d}T+\frac{RT\text{d}V}{V}\)
Similarly substituting the value of V from the equation of state, and the definition of dH we obtain the alternate form:
\(\LARGE \text{d}Q=C(\text{constant pressure})\text{d}T-\frac{RT\text{d}p}{p}\)
Substituting these forms for dQ into the differential form of the entropy equation gives:
\(\LARGE \text{d}S=C(\text{constant volume})\frac{\text{d}T}{T}+\frac{R\text{d}V}{V}\)
and
\(\LARGE \text{d}S=C(\text{constant volume})\frac{\text{d}T}{T}-\frac{R\text{d}p}{p}\)
These equations can be integrated from condition “1” to condition “2” to give:
\(\LARGE S_{2}-S_{1}=C_{v}\ln(\frac{T_{2}}{T_{1}})+R\ln(\frac{V_{2}}{V_{1}})\)
and
\(\LARGE S_{2}-S_{1}=C_{p}\ln(\frac{T_{2}}{T_{1}})-R\ln(\frac{p_{2}}{p_{1}})\)
where Cv is the heat capacity at constant volume, Cp is the heat capacity at constant pressure, and ln is the symbol for the logarithmic function.
If we divide both equations by the mass of gas, we can obtain intrinsic, or “specific” forms of both equations:
\(\LARGE s_{2}-s_{1}=c_{v}\ln(\frac{T_{2}}{T_{1}})+R\ln(\frac{v_{2}}{v_{1}})\)
and
\(\LARGE s_{2}-s_{1}=c_{p}\ln(\frac{T_{2}}{T_{1}})+R\ln(\frac{p_{2}}{p_{1}})\)
where cp and cv are the specific heat capacities. Depending on the type of process we encounter, we can now determine the change in entropy for a gas.
These equations can be a bit confusing, because we use the specific heat at constant volume when we have a process that changes volume, and the specific heat at constant pressure when the process changes pressure. To clarify matters, let’s look at the first equation:
\(\LARGE s_{2}-s_{1}=c_{v}\ln(\frac{T_{2}}{T_{1}})+R\ln(\frac{v_{2}}{v_{1}})\)
If we have a constant volume process, the second term in the equation is equal to zero, since v2/v1 = 1. We can then determine the value of the specific heat for the constant volume process. But if we have a process that changes volume, the second term in the equation is not zero. We can think of the first term of the equation as the contribution for a constant volume process, and the second term as the additional change produced by the change in volume. A similar type of argument can be made for the equation used for a change in pressure.