Center of Pressure
Velocity
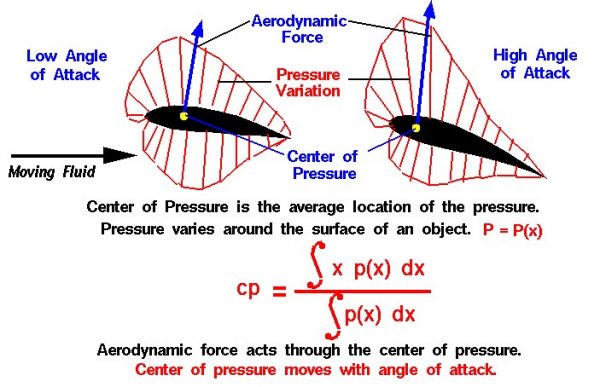
As an object moves through a fluid, the velocity of the fluid varies around the surface of the object. The variation of velocity produces a variation of pressure on the surface of the object as shown by the the thin red lines on the figure. Integrating the pressure times the surface area around the body determines the aerodynamic force on the object. We can consider this single force to act through the average location of the pressure on the surface of the object. We call the average location of the pressure variation the center of pressure in the same way that we call the average location of the weight of an object the center of gravity. The aerodynamic force can then be resolved into two components, lift and drag, which act through the center of pressure in flight.
Center of Pressure
Determining the center of pressure is very important for any flying object. To trim an airplane, or to provide stability for a model rocket or a kite, it is necessary to know the location of the center of pressure of the entire aircraft. How do engineers determine the location of the center of pressure for an aircraft which they are designing?
In general, determining the center of pressure (cp) is a very complicated procedure because the pressure changes around the object. Determining the center of pressure requires the use of calculus and a knowledge of the pressure distribution around the body. We can characterize the pressure variation around the surface as a function p(x) which indicates that the pressure depends on the distance x from a reference line usually taken as the leading edge of the object. If we can determine the form of the function, there are methods to perform a calculus integration of the equation. We will use the symbols “S[ ]dx” to denote the integration of a continuous function. Then the center of pressure can be determined from:
cp = (S[x * p(x)]dx) / (S[p(x)]dx)
If we don’t know the actual functional form, we can numerically integrate the equation using a spreadsheet by dividing the distance into a number of small distance segments and determining the average value of the pressure over that small segment. Taking the sum of the average value times the distance times the distance segment divided by the sum of the average value times the distance segment will produce the center of pressure.
Angle of Attack
There are several important problems to consider when determining the center of pressure for an airfoil. As we change angle of attack, the pressure at every point on the airfoil changes. And, therefore, the location of the center of pressure changes as well. The movement of the center of pressure caused a major problem for early airfoil designers because the amount (and sometimes the direction) of the movement was different for different designs. In general, the pressure variation around the airfoil also imparts a torque, or “twisting force”, to the airfoil. If a flying airfoil is not restrained in some way it will flip as it moves through the air. (As a further complication, the center of pressure also moves because of viscosity and compressibility effects on the flow field. But let’s save that discussion for another page.)
Aerodynamic Force
To resolve some of these design problems, aeronautical engineers prefer to characterize the forces on an airfoil by the aerodynamic force, described above, coupled with an aerodynamic moment to account for the torque. It was found both experimentally and analytically that, if the aerodynamic force is applied at a location 1/4 chord back from the leading edge on most low speed airfoils, the magnitude of the aerodynamic moment remains nearly constant with angle of attack. Engineers call the location where the aerodynamic moment remains constant the aerodynamic center of the airfoil. Using the aerodynamic center as the location where the aerodynamic force is applied eliminates the problem of the movement of the center of pressure with angle of attack in aerodynamic analysis. (For supersonic airfoils, the aerodynamic center is nearer the 1/2 chord location.)
When computing the trim of an aircraft, model rocket, or kite, we usually apply the aerodynamic forces at the aerodynamic center of airfoils and compute the center of pressure of the vehicle as an area-weighted average of the centers of the components.