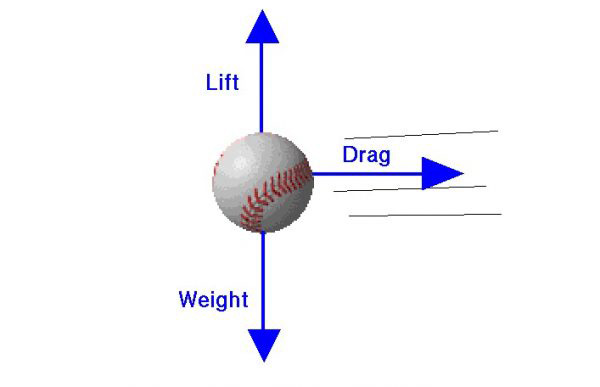
Forces on a Baseball
When a baseball is thrown or hit, the resulting motion of the ball is determined by Newton’s laws of motion. From Newton’s first law, we know that the moving ball will stay in motion in a straight line unless acted on by external forces. A force, which is a vector quantity, may be thought of as a push or pull in a specific direction. If the initial velocity and direction are known, and we can determine the magnitude and direction of all the forces on the ball, then we can predict the flight path using Newton’s laws.
There are three forces that act on a baseball in flight. The forces are the weight, drag, and lift. Lift and drag are actually two components of a single aerodynamic force acting on the ball. Drag acts in a direction opposite to the motion, and lift acts perpendicular to the motion. Let’s consider each of these forces separately.
Weight
Weight is a force that is always directed toward the center of the earth. In general, the magnitude of the weight depends on the mass of an object as determined by Newton’s law of gravitation. By rule, the weight of a major league baseball is 5 ounces. A baseball is made with a solid core, a string wrapping around the core, and a stitched covering, so the weight is distributed throughout the ball. But we can often think of the weight as collected and acting through a single point called the center of gravity. The center of gravity is the average location of the weight of an object. To first order, the center of gravity for a baseball is located at the exact center of the ball. In flight, the ball rotates about the center of gravity. Newton’s laws of motion describe the translation of the center of gravity. The physics describing the rotation, translation, weight and center of gravity of a baseball is the same for any ball. A softball is larger and slightly heavier (6.25 ounces) than a baseball. So the trajectory of a batted softball will be similar, but not the same as a batted baseball. In the software described below, the student can vary the type of ball to see the difference that weight produces in the flight of a ball.
Strictly speaking, the weight of the ball should not be specified in ounces. The ounce(oz.) is a measure of mass and not of weight. Weight is a force, mass times acceleration, and is not equal to the mass of an object. The pound is a measure of force. Unfortunately, people often use the units for weight and mass interchangeably; the assumption being that we are talking about the weight at the surface of the Earth where the acceleration is a constant (32.2 ft/sec^2 or 9.8 m/sec^2). So when the rule states that the ball weighs 5 oz, it should more correctly specify that the weight is 5/16 lb. At NASA, we have to be very careful of the distinction between mass and weight. On Mars, the mass of a baseball is the same as on Earth. But since the gravitational acceleration on Mars is 1/3 that of the Earth, the weight of a baseball on Mars is only 5/48 lb.
Drag
As the ball moves through the air, the air resists the motion of the ball and the resistance force is called drag. Drag is directed along and opposed to the flight direction. In general, there are many factors that affect the magnitude of the drag force including the shape and size of the object, the square of the velocity of the object, and conditions of the air; particularly, the density and viscosity of the air. Determining the magnitude of the drag force is difficult because it depends on the details of how the flow interacts with the surface of the object. For a baseball, this is particularly difficult because the stitches used to hold the ball together are not uniformly or symmetrically distributed around the ball. Depending on the orientation of the ball in flight, the drag changes as the flow is disturbed by the stitches. To determine the magnitude of the drag, aerodynamicists normally use a wind tunnel to measure the drag on a model. For a baseball, the drag can be determined experimentally by throwing the ball and accurately measuring the change in velocity as the ball passes between two points of known distance. A softball is slightly larger than a baseball, so the magnitude of the drag force will be different for a softball. Students can use the software mentioned below to study these differences.
Lift
Lift is the component of the aerodynamic force that is perpendicular to the flight direction. Airplane wings generate lift to overcome the weight of the airplane and allow the airplane to fly. A rotating cylinder and a spinning ball also generate aerodynamic lift. Like the drag, the magnitude of the lift depends on several factors related to the conditions of the air and the object, and the velocity between the object and the air. For a spinning ball, the speed of rotation affects the magnitude of the aerodynamic force and the direction of the force is perpendicular to the axis of rotation.
The orientation of the axis of rotation can be varied by the pitcher when the ball is thrown. If the axis is vertical, the lift force is horizontal and the ball can be made to curve to one side. If the axis is horizontal, the lift force is vertical and the ball can be made to dive or loft depending on the direction of rotation.
The stitches on a baseball introduce some additional complexity in the generation of lift and drag. For any object, the aerodynamic force acts through the center of pressure. The center of pressure is the average location of the aerodynamic forces on an object. For an ideal, smooth ball, symmetry considerations place the the center of pressure at the center of the ball along with the center of gravity. But a baseball in flight is neither smooth nor symmetric because of the stitches. So the center of pressure for a baseball moves slightly about the center of the ball with time, depending on the orientation of the stitches. The time-varying aerodynamic force causes the ball to move erratically. This motion is the source of the “dancing” knuckleball that confuses both batters and catchers alike. To account for the complexities when making predictions of the lift, aerodynamicists make an ideal prediction using theory, and then correct the prediction using experimental data. The lift coefficient – Cl for the baseball was determined by high speed photography of the flight of a pitched ball.
The motion of the ball through the air depends on the relative strength and direction of the forces shown above. We have built two simulation packages that look at the physical problem of pitching a curve ball, and of the flight of a baseball that is hit from home plate. The curve ball problem involves all three forces with the lift force producing the side force that causes the ball to curve. The simulation calculates the magnitude of the lift force and it can be shown that even big league pitchers can not generate enough lift force to overcome the weight of the ball. There are no rising fast balls. The hit baseball problem considers only the forces of drag and weight. the simulator demonstrates the important role that atmospheric conditions play on the flight of a baseball. The flight trajectory is very different from the idealized ballistic flight that occurs when drag is neglected.
The figure on this web page was created by Elizabeth Morton, of Magnificat High School, during a “shadowing” experience at NASA Glenn during May of 2007.