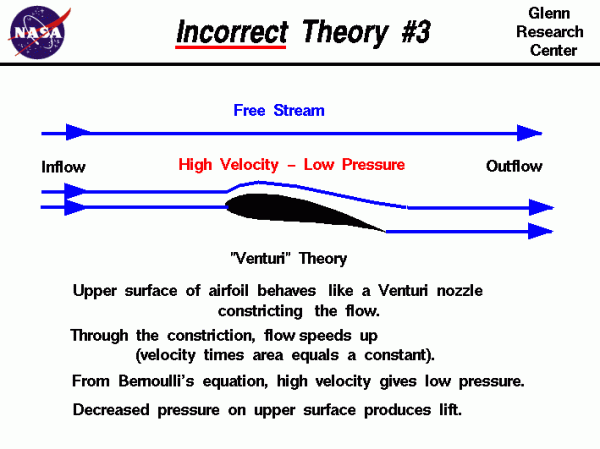
Venturi Theory

There are many theories of how lift is generated. Unfortunately, many of the theories found in encyclopedias, on web sites, and even in some textbooks are incorrect, causing unnecessary confusion for students.

The theory described on this slide is often seen on web sites and in popular literature. The theory is based on the idea that the airfoil upper surface is shaped to act as a nozzle which accelerates the flow. Such a nozzle configuration is called a Venturi nozzle and it can be analyzed classically. Considering the conservation of mass, the mass flowing past any point in the nozzle is a constant; the mass flow rate of a Venturi nozzle is a constant. The mass flow rate m dot is equal to the density r times the velocity V times the flow area A:

m dot = r * V * A = constant

For a constant density, decreasing the area increases the velocity.

Turning to the incorrect airfoil theory, the top of the airfoil is curved, which constricts the flow. Since the area is decreased, the velocity over the top of the foil is increased. Then from Bernoulli’s equation, higher velocity produces a lower pressure on the upper surface. The low pressure over the upper surface of the airfoil produces the lift.

Venturi nozzle

The theory is based on an analysis of a Venturi nozzle. But an airfoil is not a Venturi nozzle. There is no phantom surface to produce the other half of the nozzle. In our experiments we’ve noted that the velocity gradually decreases as you move away from the airfoil eventually approaching the free stream velocity. This is not the velocity found along the centerline of a nozzle which is typically higher than the velocity along the wall.

Venturi analysis

This analysis cannot predict the lift generated by a flat plate. The leading edge of a flat plate presents no constriction to the flow so there is really no “nozzle” formed. One could argue that a “nozzle” occurs when the angle of the flat plate is negative. But as we have seen in Experiment #2, this produces a negative lift. The velocity actually slows down on the upper surface at a negative angle of attack; it does not speed up as expected from the nozzle model.

This theory deals with only the pressure and velocity along the upper surface of the airfoil. It neglects the shape of the lower surface. If this theory were correct, we could have any shape we want for the lower surface, and the lift would be the same. This obviously is not the way it works – the lower surface does contribute to the lift generated by an airfoil. (In fact, one of the other incorrect theories proposed that only the lower surface produces lift!)

The part of the theory about Bernoulli’s equation and a difference in pressure existing across the airfoil is correct. In fact, this theory is very appealing because there are parts of the theory that are correct. In our discussions on pressure-area integration to determine the force on a body immersed in a fluid, we mentioned that if we knew the velocity, we could obtain the pressure and determine the force.

The problem

The problem with the “Venturi” theory is that it attempts to provide us with the velocity based on an incorrect assumption (the constriction of the flow produces the velocity field). We can calculate a velocity based on this assumption, and use Bernoulli’s equation to compute the pressure, and perform the pressure-area calculation and the answer we get does not agree with the lift that we measure for a given airfoil.