Vectored Thrust

Four Forces

There are four forces that act on an aircraft in flight: lift, weight, thrust, and drag. The motion of the aircraft through the air depends on the relative size of the various forces and the orientation of the aircraft. For an aircraft in cruise, the four forces are balanced, and the aircraft moves at a constant velocity and altitude. Some modern fighter aircraft can change the angle of the thrust by using a movable nozzle. The ability to change the angle of the thrust is called thrust vectoring, or vectored thrust.

Vector Quantities

Forces are vector quantities having a magnitude and a direction. The resulting acceleration, velocity and displacement of the aircraft are also vector quantities which can be determined by Newton’s second law of motion and the rules of vector algebra. There are two component equations for the force on an aircraft. One equation gives the the net vertical force Fv, and the other gives the net horizontal force Fh. If we denote the thrust by the symbol T, the lift by L, the drag by D, and the weight by W, the usual force equations for an aircraft in level flight are:

Vertical: L – W = Fv

Horizontal: T – D = Fh

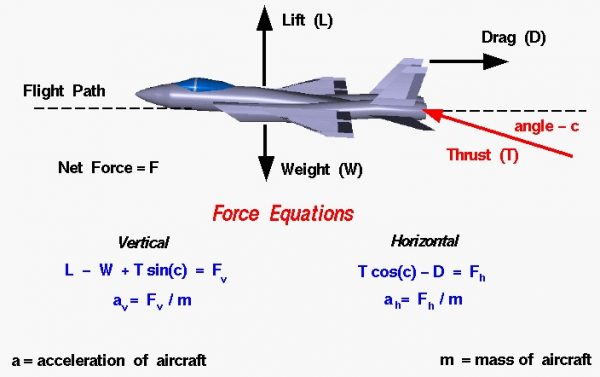
Excess Thrust

The quantity (T – D) is called the excess thrust and is related to the aircraft’s ability to accelerate. Good fighter aircraft have high excess thrust. The ability to climb and maneuver involves the vertical net force as well as the excess thrust. Since the thrust force is already a large force for fighter aircraft, designers have sought ways to bring this force into the vertical equations of motion. With new mechanical systems it is possible to deflect the engine exhaust from the nozzle and cant the thrust vector at an angle. We will call this angle c. The resulting force equations are shown on the slide:

Vertical: L – W + T sin(c) = Fv

Horizontal: T cos(c) – D = Fh

where sin and cos are the trigonometric sine and cosine functions. The thrust now appears in the vertical force equation. This allows the aircraft to climb faster than an aircraft without thrust vectoring and to execute sharper turns than an un-vectored aircraft. For moderate angles, the cos is nearly equal to one, so the aircraft still has high excess thrust. The horizontal acceleration ah and vertical acceleration av of the aircraft are given by:

av = Fv /m

ah = Fh /m

where m is the mass of the aircraft. The only serious penalty for having vectored thrust is that the nozzle is heavier than a standard nozzle.