Torque (Moment)

Force

A force may be thought of as a push or pull in a specific direction. When a force is applied to an object, the object accelerates in the direction of the force according to Newton’s laws of motion. The object may also experience a rotation depending on how the object is confined and where the force is applied. A hanging door is an excellent example of this type of motion. When you push on a door it can not freely translate because it is confined (or pinned) by the hinges. It does, however, rotate on the hinges. The rotation itself depends on where you apply the force. As you get closer to the hinge, you must apply a larger force to make the door swing. As you get farther from the hinge, you can apply a smaller force to make the door swing.

Rotation

The product of the force and the perpendicular distance to a pivot (or hinge) is called the torque or the moment. Torques produce rotations in the same way that forces produce translations. Namely, an object at rest, or rotating at a constant angular velocity continues to do so until it is subject to an external torque. A torque produces an angular acceleration or change in angular velocity. If an object is not pinned, it rotates about its center of gravity when acted upon by an external force. The distance used in the calculation of the torque is then the distance from the center of gravity perpendicular to the applied force.

Vector

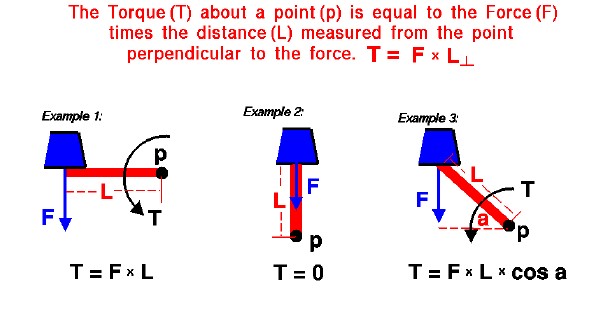
A force (F) is a vector quantity, which means that it has both a magnitude and a direction associated with it. The direction is important. A force directed due north produces a different result on an object than a force of the same magnitude, but directed to the east. The distance (L) used to determine the torque (T) is the distance from the pivot (p) to the force, but measured perpendicular to the direction of the force. We show three examples on the figure of this principle as applied to a weight (blue) which is acting on an arm (red bar). In Example 1, the force (weight) is applied perpendicular to the arm. In this case, the perpendicular distance is the actual length of the bar and the torque is equal to the product of the length and the force.

T = F * L

Pivot

In Example 2, the same force is applied to the arm, but the force now acts right through the pivot. In this case, the distance from the pivot perpendicular to the force is zero So, in this case, the torque is also zero. Think of the hinged door example; if you push on the edge of the door, towards the hinge, the door doesn’t move because the torque is zero. Example 3 is the general case in which the force is applied at some angle a to the arm. The perpendicular distance is given by trigonometry as the length of the arm (L) times the cosine (cos) of the angle.

T = F * L * cos(a)

Examples

Examples 1 and 2 can be derived from this general formula, since the cosine of 0 degrees is 1.0 (Example 1), and the cosine of 90 degrees is 0.0 (Example 2).

Control Surfaces

The Wright brothers used the torque generated by aerodynamic surfaces to stabilize and control their aircraft. On an airplane, each control surfaces produces aerodynamic lift and drag. These forces are applied at some distance from the aircraft center of gravity and therefore cause the aircraft to rotate. The elevators produce a pitching moment, the rudder produce a yawing moment, and the wing warping produced a rolling moment. The ability to vary the amount of the force and the moment allowed the pilot to maneuver the aircraft.