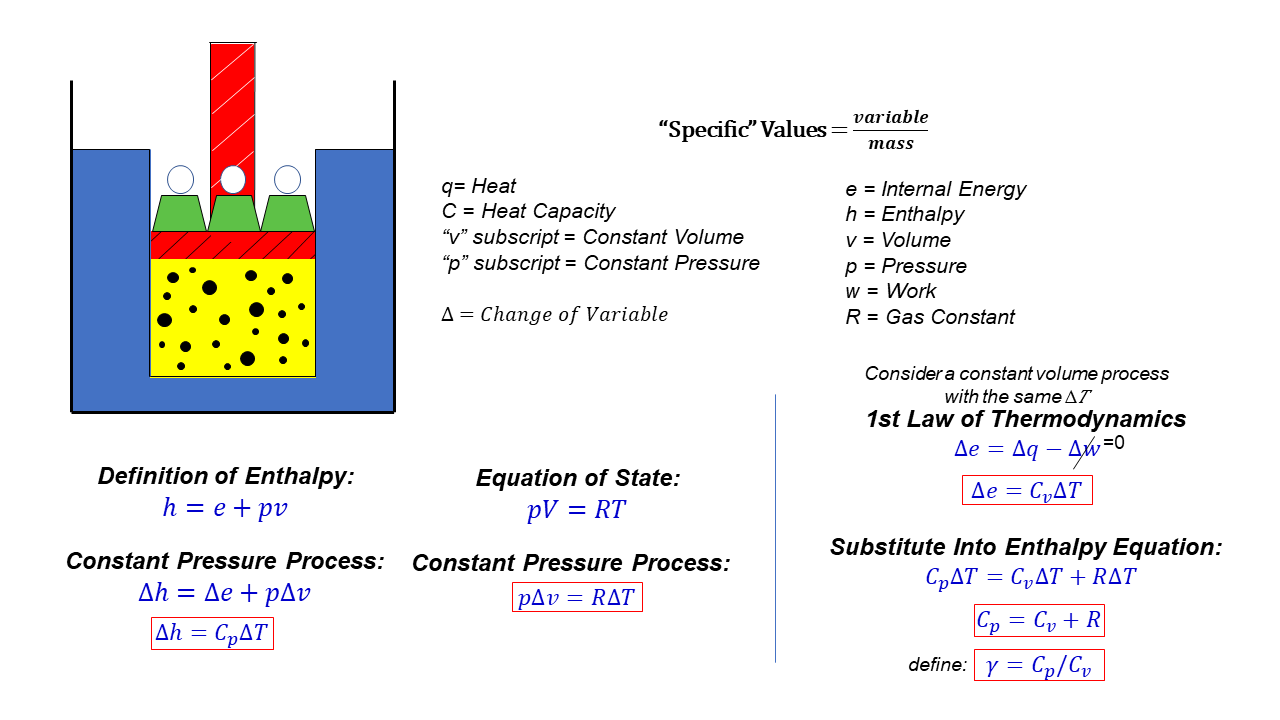
Specific Heats – cp and cv

Thermodynamics is a branch of physics which deals with the energy and work of a system. Thermodynamics deals only with the large-scale response of a system which we can observe and measure in experiments. Like the Wright brothers, we are most interested in thermodynamics for the role it plays in engine design.

On this page we derive some equations which relate the heat capacity of a gas to the gas constant used in the equation of state. We are going to be using specific values of the state variables. For a scientist, a “specific” state variable means the value of the variable divided by the mass of the substance. This allows us to derive relations between variables without regard for the amount of the substance that we have. We can multiply the specific variable by the quantity of the substance at any time to determine the actual value of the flow variable.

From our studies of heat transfer, we know that the amount of heat transferred between two objects is proportional to the temperature difference between the objects and the heat capacity of the objects. The heat capacity is a constant that tells how much heat is added per unit temperature rise. The value of the constant is different for different materials and depends on the process. Heat capacity is not a state variable.

If we are dealing with a gas, it is most convenient to use forms of the thermodynamics equations based on the enthalpy of the gas. From the definition of enthalpy:

h = e + p * v

where h in the specific enthalpy, p is the pressure, v is the specific volume, and e is the specific internal energy. During a process, the values of these variables will change. Let’s denote the change by the Greek letter delta (which looks like a triangle). So “delta h” means the change of “h” from state 1 to state 2 during a process. Then, for a constant pressure process the enthalpy equation becomes:

delta h = delta e + p * delta v

The enthalpy, internal energy, and volume are all changed, but the pressure remains the same. From our derivation of the enthalpy equation, the change of specific enthalpy is equal to the heat transfer for a constant pressure process:

delta h = cp * delta T

where delta T is the change of temperature of the gas during the process, and c is the specific heat capacity. We have added a subscript “p” to the specific heat capacity to remind us that this value only applies to a constant pressure process.

The equation of state of a gas relates the temperature, pressure, and volume through a gas constant R. The gas constant used by aerodynamicists is derived from the universal gas constant but has a unique value for every gas.

p * v = R * T

If we have a constant pressure process, then:

p * delta v = R * delta T

Now let us imagine that we have a constant volume process with our gas that produces exactly the same temperature change as the constant pressure process that we have been discussing. Then the first law thermodynamics tells us:

delta e = delta q – delta w

where q is the specific heat transfer and w is the work done by the gas. For a constant volume process, the work is equal to zero. And we can express the heat transfer as a constant times the change in temperature. This gives:

delta e = cv * delta T

where delta T is the change of temperature of the gas during the process, and c is the specific heat capacity. We have added a subscript “v” to the specific heat capacity to remind us that this value only applies to a constant volume process. Even though the temperature change is the same for this process and the constant pressure process, the value of the specific heat capacity is different.

Because we have selected the constant volume process to give the same change in temperature as our constant pressure process, we can substitute the expression given above for “delta e” into the enthalpy equation. In general, you can’t make this substitution because a constant pressure process and a constant volume process will produce different changes in temperature.

If we substitute the expressions for “delta e”, “p * delta v”, and “delta h” into the enthalpy equation we obtain:

cp * delta T = cv * delta T + R * delta T

dividing by “delta T” gives the relation:

cp = cv + R

The specific heat constants for constant pressure and constant volume processes are related to the gas constant for a given gas. This rather remarkable result has been derived from thermodynamic relations, which are based on observations of physical systems and processes. In the kinetic theory of gases, this result is derived from considerations of the conservation of energy at a molecular level.

We can define an additional variable called the ratio of specific heats, which is given the Greek symbol “gamma”, which is equal to cp divided by cv:

gamma = cp / cv

“Gamma” is just a number whose value depends on the state of the gas. For air, gamma = 1.4 for standard day conditions. “Gamma” appears in several equations which relate pressure, temperature, and volume during a simple compression or expansion process. Because the value of “gamma” just depends on the state of the gas, there are tables of these values for given gases. You can use the tables to solve gas dynamics problems.