Second Law – Entropy
Thermodynamics is a branch of physics which deals with the energy and work of a system. Thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. In aerodynamics, the thermodynamics of a gas obviously plays an important role in the analysis of propulsion systems. The first law of thermodynamics defines the relationship between the various forms of kinetic and potential energy present in a system, the work which the system can perform and the transfer of heat. The law states that energy is conserved in all thermodynamic processes.
However, we can imagine thermodynamic processes which would conserve energy but which never occur in nature. For example, if we bring a hot object into contact with a cold object, the hot object cools down and the cold object heats up until an equilibrium is reached. The transfer of heat goes from the hot object to the cold object. We could imagine a system in which the heat would instead be transferred from the cold object to the hot object, and such a system would not violate the first law of thermodynamics. The cold object would get colder and the hot object would get hotter but energy would be conserved. Obviously we don’t encounter such a system in nature and to explain this and similar observations, thermodynamicists proposed a second law of thermodynamics. Clasius, Kelvin, and Carnot proposed various forms of the second law to describe the particular physics problem that each was studying. The description of the second law stated on this slide was taken from Halliday and Resnick’s textbook, “Physics”. It begins with the definition of a new state variable called entropy. Entropy has a variety of physical interpretations, including the statistical disorder of the system, but for our purposes, let us consider entropy to be just another property of the system, like enthalpy or temperature.
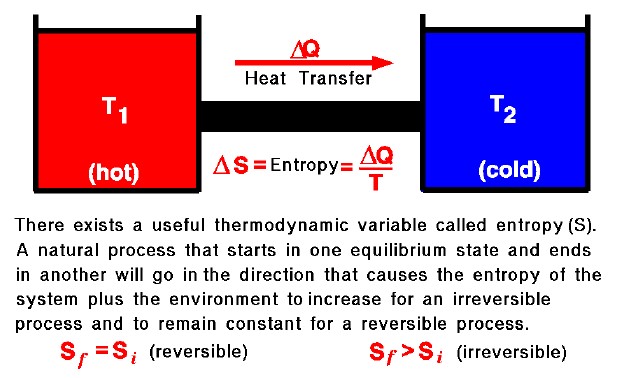
The second law states that there exists a useful state variable called entropy. The change in entropy (delta S, \(\Delta S\)) is equal to the heat transfer (delta Q, \(\Delta Q\)) divided by the temperature (T).
\(\LARGE \Delta S=\frac{\Delta Q}{T}\)
For a given physical process, the entropy of the system and the environment will remain a constant if the process can be reversed. If we denote the initial and final states of the system by “i” and “f”, then:
\(\LARGE S_{f}=S_{i}(\text{reversible process})\)
An example of a reversible process would be ideally forcing a flow through a constricted pipe. (Ideal means no boundary layer losses). As the flow moves through the constriction, the pressure, temperature and velocity would change, but these variables would return to their original values downstream of the constriction. The state of the gas would return to its original conditions and the change of entropy of the system would be zero. The second law states that if the physical process is irreversible, the entropy of the system and the environment must increase; the final entropy must be greater than the initial entropy.
\(\LARGE S_{f}>S_{i}(\text{reversible process})\)
An example of an irreversible process is the problem discussed in the second paragraph where a hot object is put in contact with a cold object. Eventually, they both achieve the same equilibrium temperature. If we then separate the objects they do not naturally return to their original (different) temperatures. The process of bringing them to the same temperature is irreversible.
The application of the second law describes why heat is transferred from the hot object to the cool object. Let us assume that the heat is transferred from the hot object (object 1) at temperature T1 to the cold object (object 2) at temperature T2. The amount of heat transferred is Q and the final equilibrium temperature for both objects we will call Tf. The temperature of the hot object changes as the heat is transferred away from the object. The average temperature of the hot object during the process we will call Th and it would be the average of T1 and Tf.
\(\LARGE T_{h}=\frac{T_{1}+T_{f}}{2}\)
Similarly, for the cold object, the final temperature is Tf and the average temperature during the process is Tc which is the average of Tf and T2.
\(\LARGE T_{c}=\frac{T_{2}+T_{f}}{2}\)
Th will always be greater than Tc, because T1 is greater than T2.
\(\LARGE T_{h}>T_{c}\)
The entropy change for the hot object will be (-Q/Th), with the minus sign applied because the heat is transferred away from the object.
\(\LARGE \Delta S_{h}=-\frac{Q}{T_{h}}\)
For the cold object, the entropy change is (Q/Tc), positive because the heat is transferred into the object.
\(\LARGE \Delta S_{c}=\frac{Q}{T_{c}}\)
So the total entropy change for the whole system would be given by the equation
\(\LARGE S_{f}=S_{i}-\frac{Q}{T_{h}}+\frac{Q}{T_{c}}\)
with Si and Sf being the final and initial values of the entropy. The term (Q/Tc) will always be greater than (-Q/Th) because Th is greater than Tc. Therefore, Sf will be greater than Si, as the second law predicts. If, instead, we had assumed that the heat was being transferred from the cold object to the hot object, our final equation would be:
\(\LARGE S_{f}=S_{i}+\frac{Q}{T_{h}}-\frac{Q}{T_{c}}\)
The signs on the terms would be changed because of the direction of the heat transfer. This would result in Sf being less than Si and the entropy of the system would decrease which would violate the second law of thermodynamics.
