Pitot – Static Tube – Speedometer
Pitot-Static Tubes
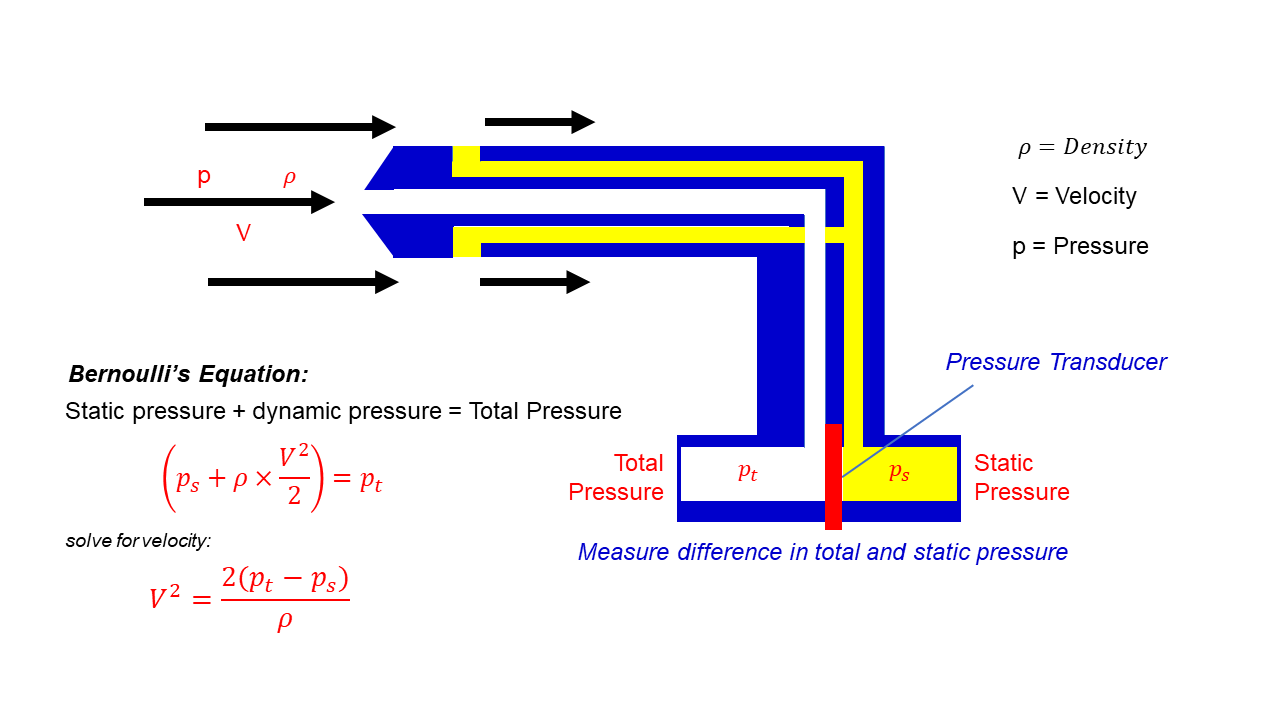
This page shows a schematic drawing of a pitot-static tube. Pitot-Static tubes, which are also called Prandtl tubes, are used on aircraft as speedometers. The actual tube on the aircraft is around 10 inches (25 centimeters) long with a 1/2-inch (1 centimeter) diameter. Several small holes are drilled around the outside of the tube and a center hole is drilled down the axis of the tube. The outside holes are connected to one side of a device called a pressure transducer. The center hole in the tube is kept separate from the outside holes and is connected to the other side of the transducer. The transducer measures the difference in pressure in the two groups of tubes by measuring the strain in a thin element using an electronic strain gauge.
The pitot-static tube is mounted on the aircraft, or in a wind tunnel, so that the center tube is always pointed in the direction of the flow and the outside holes are perpendicular to the center tube. On some airplanes the pitot-static tube is put on a longer boom sticking out of the nose of the plane or the wing.
Difference in Static and Total Pressure
Since the outside holes are perpendicular to the direction of flow, these tubes are pressurized by the local random component of the air velocity. The pressure in these tubes is the static pressure (ps) discussed in Bernoulli’s equation. The center tube, however, is pointed in the direction of travel and is pressurized by both the random and the ordered air velocity. The pressure in this tube is the total pressure (pt) discussed in Bernoulli’s equation. The pressure transducer measures the difference in total and static pressure which is the dynamic pressure q.
measurement = q = pt – ps
Solve for Velocity
With the difference in pressures measured and knowing the local value of air density from pressure and temperature measurements, we can use Bernoulli’s equation to give us the velocity. On the graphic, the Greek symbol rho is used for the air density. In this text, we will use the letter r. Bernoulli’s equation states that the static pressure plus one half the density times the velocity V squared is equal to the total pressure.
ps + .5 * r * V ^2 = pt
Solving for V:
V ^2 = 2 * {pt – ps} / r
V = sqrt [2 * {pt – ps} / r ]
where sqrt denotes the square root function.
Limitations
There are some practical limitations to the use of a pitot-static tube:
- If the velocity is low, the difference in pressures is very small and hard to accurately measure with the transducer. Errors in the instrument could be greater than the measurement! So pitot-static tubes don’t work very well for very low velocities.
- If the velocity is very high (supersonic), we’ve violated the assumptions of Bernoulli’s equation and the measurement is wrong again. At the front of the tube, a shock wave appears that will change the total pressure. There are corrections for the shock wave that can be applied to allow us to use pitot-static tubes for high-speed aircraft.
- If the tubes become clogged or pinched, the resulting pressures at the transducer are not the total and static pressures of the external flow. The transducer output is then used to calculate a velocity that is not the actual velocity of the flow. Several years ago, there were reports of icing problems occurring on airliner pitot-static probes. Output from the probes was used as part of the autopilot and flight control system. The solution to the icing problem was to install heaters on the probes to ensure that the probes were not clogged by ice build-up.
Notice – In using this equation to determine the velocity, we must be very careful and use the proper units of measure. The air density must be specified as mass / volume (kg/m^3 or slug/ft^3) while the pressure is specified as force / area (Pa or lbs/ft^2).