Lift to Drag (L/D) Ratio

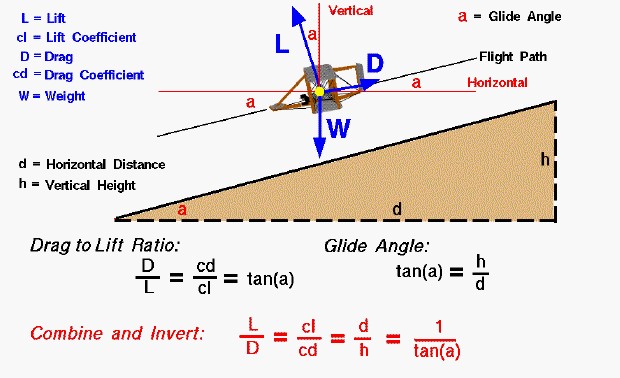
This slide shows the balance of forces on a descending Wright 1902 glider. The flight path of the glider is along the thin black line, which falls to the left. The flight path intersects the horizontal, thin, red line at an angle “a” called the glide angle.

The tangent of the glide angle, tan(a), is equal to the vertical height (h) which the aircraft descends divided by the horizontal distance (d) which the aircraft flies across the ground.

tan(a) = h / d

The tangent of the glide angle is also related to the ratio of the drag, D, of the the aircraft to the lift, L.

D / L = cd / cl = tan(a)

Where cd and cl are the drag and lift coefficients derived from the drag and lift equations and measured during wind tunnel testing.

What good is all this for aircraft design? If we combine the two equations into a single equation through the tan(a), and invert the equation, we get:

L / D = cl / cd = d / h = 1 / tan(a)

The lift divided by drag is called the L/D ratio, pronounced “L over D ratio.” From the last equation we see that the higher the L/D, the lower the glide angle, and the greater the distance that a glider can travel across the ground for a given change in height. Because lift and drag are both aerodynamic forces, we can think of the L/D ratio as an aerodynamic efficiency factor for the aircraft. Designers of gliders and designers of cruising aircraft want a high L/D ratio to maximize the distance which an aircraft can fly. It is not enough to just design an aircraft to produce enough lift to overcome weight. The designer must also keep the L/D ratio high to maximize the range of the aircraft.

We could have used D/L as the efficiency factor, but then the lower the factor the better the aircraft. Engineers usually define efficiency factors so that “bigger” is “better”.