Lift Equation

Lift

Lift depends on the density of the air, the square of the velocity, the air’s viscosity and compressibility, the surface area over which the air flows, the shape of the body, and the body’s inclination to the flow. In general, the dependence on body shape, inclination, air viscosity, and compressibility is very complex.

Lift Coefficient

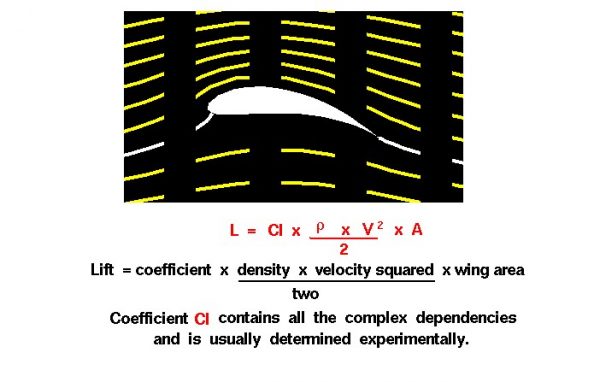
One way to deal with complex dependencies is to characterize the dependence by a single variable. For lift, this variable is called the lift coefficient, designated “Cl.” This allows us to collect all the effects, simple and complex, into a single equation. The lift equation states that lift L is equal to the lift coefficient Cl times the density rho (\(\bf\rho\)) times half of the velocity V squared times the wing area A.

\(\LARGE L=\mathit{Cl}\frac{\rho V^{2}}{2}A\)

Flow Conditions

For given air conditions, shape, and inclination of the object, we have to determine a value for Cl to determine the lift. For some simple flow conditions and geometries and low inclinations, aerodynamicists can determine the value of Cl mathematically. But, in general, this parameter is determined experimentally.

Density

In the equation given above, the density is designated by the letter \(\rho\). We do not use “d” for density, since “d” is often used to specify distance. In many textbooks on aerodynamics, the density is given by the Greek symbol “rho” (Greek for “r”). The combination of terms “density times the square of the velocity divided by two” is called the dynamic pressure and appears in Bernoulli’s pressure equation.