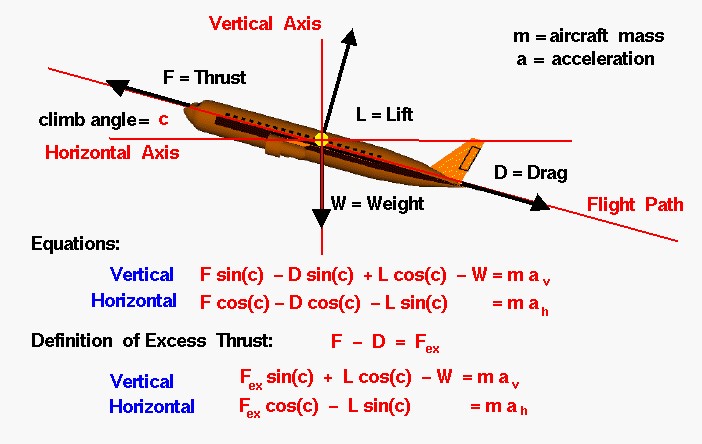
Forces in a Climb

Four Forces

There are four forces that act on an aircraft in flight: lift, weight, thrust, and drag. The motion of the aircraft through the air depends on the relative size of the various forces and the orientation of the aircraft. For an aircraft in cruise, the four forces are balanced, and the aircraft moves at a constant velocity and altitude. On this slide, we consider the relations of the forces during a gradual climb.

We have drawn a vertical and horizontal axis on our aircraft through the center of gravity. A red line inclined to the horizontal at angle c shows the flight path. The lift and drag are aerodynamic forces that are defined relative to the flight path. The lift is perpendicular to the flight path and the drag is along the flight path. The thrust of the aircraft is also usually aligned with the flight path. Some modern fighter aircraft can change the angle of the thrust, but we are going to assume that the thrust is along the flight path direction. The weight of an airplane is always directed towards the center of the Earth and is, therefore, along the vertical axis.

Vector Quantities

Forces are vector quantities. We can write two component equations for the motion of the aircraft based on Newton’s second law of motion and the rules of vector algebra. One equation gives the vertical acceleration av, and the other gives the horizontal acceleration ah in terms of the components of the forces and the mass m of the aircraft. If we denote the thrust by the symbol F, the lift by L, the drag by D, and the weight by W, the vertical component equation is:

F * sin(c) – D * sin(c) + L * cos(c) – W = m * av

where sin and cos are the trigonometric sine and cosine functions. Similarly, the horizontal component equation is:

F * cos(c) – D * cos(c) – L * sin(c) = m * ah

We can simplify the equations a little by using the definition of excess thrust Fex:

Fex = F – D

The resulting equations of motion are:

Vertical: Fex * sin(c) + L * cos(c) – W = m * av

Horizontal: Fex * cos(c) – L * sin(c) = m * ah

For small climb angles, the cos(c) is nearly 1.0 and the sin(c) is nearly zero. The equations then reduce to:

Vertical: L – W = m * av

Horizontal: F – D = m * ah

Thrust

For more moderate angles, high excess thrust can provide an important contribution to the vertical acceleration. The next time you visit an airport, notice the high climb angles used by modern airliners. This flight path is possible because modern turbine engines develop high excess thrust at takeoff. The pilot climbs sharply to get the aircraft as high as possible within the confines of the airport which produces the least noise for homes near the airport.