Flight Equations with Drag
A ball in flight has no engine to produce thrust, so the resulting flight is similar to the flight of shell from a cannon, or a bullet from a gun. This type of flight is called ballistic flight and assumes that weight is the only force acting on the ball. In reality, a baseball or a soccer ball in flight generates a moderate amount of aerodynamic drag and is not strictly ballistic. On this page we develop the equations which describe the motion of a flying ball including the effects of drag.
Vertical Location
At launch the ball is inclined at some angle to the vertical, so we resolve the initial velocity into a vertical and horizontal component. Unlike the ballistic flight equations, the horizontal equation includes the action of aerodynamic drag on the ball. We will first consider the vertical component and then develop the equations for the horizontal component.
In the vertical plane, the only forces acting on the ball are the forces of weight and drag. There is a characteristic velocity which appears in many of the equations that is called the terminal velocity because it is the constant velocity that the object sustains during a coasting descent. Terminal velocity is noted by the symbol Vt.
Vertical Descent
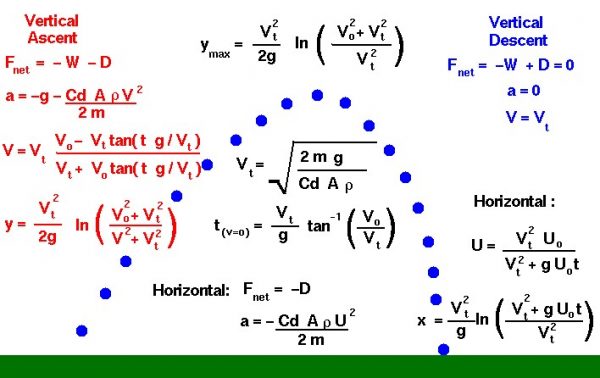
During the vertical descent, for a light object, the weight and drag of an object are equal and opposite. There is no net force acting on the ball and the vertical acceleration is zero.
\(\LARGE a=0\)
\(\LARGE W=D\)
where a is the acceleration, W is the weight, and D is the drag. The weight of any object is given by the weight equation:
\(\LARGE W=mg\)
where m is the mass of the object and g is the gravitational acceleration equal to 32.2 ft/sec2 or 9.8 m/sec2 on the surface of the Earth. (The gravitational acceleration has different values on the Moon and on Mars.) The drag is given by the drag equation:
\(\LARGE D=\frac{\mathit{Cd}\cdot\rho AV_{t}^{2}}{2}\)
where rho (\(\bf\rho\)) is the gas density, Cd is the drag coefficient which characterizes the effects of shape of the ball, A is the cross-sectional area of the ball, and Vt is the terminal velocity.
Velocity
The gas density has different surface values on the Earth and on Mars and varies with altitude. On the Moon the gas density is zero. Combining the last three equations, we can determine the terminal velocity:
\(\LARGE mg=\frac{\mathit{Cd}\cdot\rho AV_{t}^2}{2}\)
\(\LARGE V_{t}=\sqrt{\frac{2mg}{\mathit{Cd}\cdot\rho A}}\)
Now, turning to the ascent trajectory, the ball is traveling at an initial vertical velocity V0. With the positive vertical coordinate denoted by y, the net vertical force Fnet acting on the ball is given by:
\(\LARGE F_{net}=-W-D\)
Because the weight of the object is a constant, we can use the simple form of Newton’s second law to solve for the vertical acceleration:
\(\LARGE F_{net}=ma=-W-D\)
\(\LARGE ma=-mg-\frac{\mathit{Cd}\cdot\rho Av^{2}}{2}\)
\(\LARGE a=-g-\frac{\mathit{Cd}\cdot\rho Av^{2}}{2m}\)
Notice that the acceleration changes with time. Multiply the last term by \(\bf \frac{g}{g}\) and use the definition of the terminal velocity to obtain:
\(\LARGE a=-g\frac{1+v^{2}}{V_{t}^2}\)
Acceleration
The acceleration is the time rate of change of velocity:
\(\LARGE a=\frac{\text{d}v}{\text{d}t}=-g\frac{1+v^{2}}{V_{t}^{2}}\)
Integrating this differential equation:
\(\LARGE \frac{{\text{d}v}}{\frac{1+v^{2}}{V_{t}^{2}}}=-g{\text{d}t}\)
\(\LARGE V_{t}\tan^{-1}(\frac{v}{V_{t}})=-gt\)
where tan-1 is the inverse tangent function, and t is time. The limits of integration for velocity v are from V0 to V and the limits for time t is from 0 to t:
\(\LARGE \tan^{-1}(\frac{V}{V_{t}})-\tan^{-1}(\frac{V_{0}}{V_{t}})=\frac{-gt}{V_{t}}\)
\(\LARGE \tan^{-1}(\frac{V}{V_{t}})=\tan^{-1}(\frac{V_{0}}{V_{t}})-\frac{gt}{V_{t}}\)
Now take the tangent function of both sides of the equation using the trigonometric identity:
\(\LARGE \tan(a-b)=\frac{\tan(a)-\tan(b)}{1+\tan(a)\tan(b)}\)
on the right-hand side to obtain:
\(\LARGE \frac{V}{V_{t}}=\frac{\frac{V_{0}}{V_{t}}-\tan(\frac{gt}{V_{t}})}{1+\frac{V_{0}}{V_{t}}\tan(\frac{gt}{V_{t}})}\)
\(\LARGE \frac{V}{V_{t}}=\frac{V_{0}-V_{t}-\tan(\frac{gt}{V_{t}})}{V_{t}+V_{0}\tan(\frac{gt}{V_{t}})}\)
Vertical Ascent
This is the equation for the velocity at any time during the vertical ascent. At the top of the trajectory, the velocity is zero. We can solve the velocity equation to determine the time when this occurs:
\(\LARGE \frac{V_{0}}{V_{t}}=\tan(\frac{gt(v=0)}{V_t})\)
\(\LARGE t(v=0)=\frac{V_{t}}{g}\tan^{-1}(\frac{V_{0}}{V_{t}})\)
To determine the vertical location during the ascent, we have to use another identity from differential calculus:
\(\LARGE \frac{\text{d}v}{\text{d}t}=\frac{\text{d}v}{\text{d}y}\cdot\frac{\text{d}y}{\text{d}t}\)
\(\LARGE \frac{\text{d}v}{\text{d}t}=v\frac{\text{d}v}{\text{d}y}\)
We previously determined that:
\(\LARGE \frac{\text{d}v}{\text{d}t}=-g\frac{1+v^{2}}{V_t^{2}}\)
\(\LARGE v\frac{\text{d}v}{\text{d}y}=-g\frac{1+v^{2}}{V_{t}^{2}}\)
\(\LARGE \frac{v}{\frac{1+v^{2}}{V_{t}^2}}\text{d}v=-g\text{d}y\)
Integrating both sides:
\(\LARGE \frac{V_{t}^2}{2}\ln(v^{2}+V_{t}^{2})=-gy\)
where ln is the natural logarithmic function. The limits of integration for velocity v is from V0 to V and the limits for direction y is from 0 to y:
\(\LARGE \frac{V_{t}^2}{2}\ln(V^{2}+V_{t}^2)-\ln(V_{0}^2+V_{t}^2)=-gy\)
\(\LARGE y=\frac{V_{t}^{2}}{2g}\ln(\frac{V_{0}^2+V_{t}^{2}}{V^{2}+V_{t}^{2}})\)
Notice that the location equation is pretty messy! For a given time t, we would have to find the local velocity V, and then plug that value into the location equation to get the location y. At the maximum height ymax, the velocity is equal to zero:
\(\LARGE y_{max}=\frac{V_{t}^{2}}{2g}\ln(\frac{V_{0}^{2}+V_{t}^{2}}{V_{t}^{2}})\)
Horizontal Location
The horizontal equations are a little easier, since the only net force acting on the ball is the drag:
\(\LARGE F_{net}=ma=-D\)
\(\LARGE ma=-\frac{\mathit{Cd}\cdot\rho Au^{2}}{2}\)
\(\LARGE a=-\frac{\mathit{Cd}\cdot\rho Au^{2}}{2m}\)
where u is the horizontal velocity. We can use the terminal velocity to simplify this equation:
\(\LARGE a=\frac{\text{d}u}{\text{d}t}=\frac{-gu^{2}}{V_{t}^2}\)
\(\LARGE \frac{1}{u^{2}}{\text{d}u}=-\frac{g}{V_{t}^{2}}{\text{d}t}\)
Integrating the equations, with the limits on the velocity from the initial velocity U0 to U, we obtain:
\(\LARGE u=\frac{\text{d}x}{\text{d}t}=\frac{V_{t}^{2}U_{0}}{V_{t}^2+gU_{0}t}\)
The horizontal velocity is inversely dependent on the time. We can similarly solve for the location x at any time by integrating the velocity equation:
\(\LARGE x=\frac{V_{t}^{2}}{g}\ln(\frac{V_{t}^{2}+gU_{0}t}{V_{t}^2})\)
