First Law – Conservation of Energy

The conservation of energy is a fundamental concept of physics along with the conservation of mass and the conservation of momentum. Within some problem domain, the amount of energy remains constant and energy is neither created nor destroyed. Energy can be converted from one form to another (potential energy can be converted to kinetic energy) but the total energy within the domain remains fixed. On some separate slides, we have discussed the state of a static gas, the properties which define the state, and the first law of thermodynamics as applied to any system, in general. On this slide we derive a useful form of the energy conservation equation for a gas beginning with the first law of thermodynamics.

Thermodynamics is a branch of physics which deals with the energy and work of a system. Thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. Like the Wright brothers, we are most interested in thermodynamics in the study of propulsion systems. Aeronautical engineers usually simplify a thermodynamic analysis by using intensive variables; variables that do not depend on the mass of the gas. We call these variables specific variables, and many of the state properties listed on this slide, such as the work, internal energy, and volume are specific quantities; the value of the quantity divided by the mass of the quantity. Engineers usually use the lower case letter for the “specific” version of a variable.

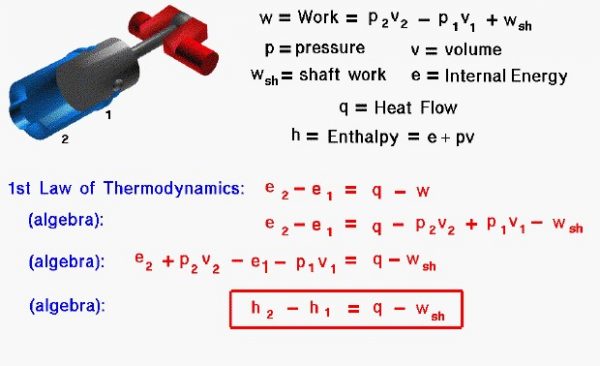
Let us look at the state variables present in a sample problem. The figure shows a piston in a cylinder of the Wright 1903 engine. As the piston moves from position 1 to position 2, it compresses the gas present in the cylinder. Work (w) is performed on the gas. Some of the work, called the shaft work (wsh), opposes the motion of the cylinder, while the rest of the work goes into changing the state of the gas. The work performed to change the state of the gas is equal to the difference in the pressure (p) times the specific volume (v) from state 1 to state 2.

w = wsh + p2 * v2 – p1 * v1

The specific internal energy (e) is defined by the first law of thermodynamics. Although it is not present in this problem, heat (q) may also be transferred to the gas. From the first law of thermodynamics, the change in internal energy is equal to heat transfer minus the work.

e2 – e1 = q – w

A useful additional variable, called the specific enthalpy (h), is the sum of the internal energy and the pressure-volume term used to define the work on the gas.

h = e + p * v

If we perform a little algebra on the first law of thermodynamics, we can begin to group some terms of the equations. In particular, the enthalpy of the gas can be used to simplify the equation into its final form:

h2 – h1 = q – wsh

For the compression stroke and power stroke of a four-stroke engine, there is no external heat flow into the gas and the “q” term is set equal to zero. During combustion, no work is performed and the “wsh” term is set to zero.