Equilibrium

Vector

A very basic concept when dealing with either forces or torques (moments) is the idea of equilibrium or balance. Forces and torques are vector quantities which means that they have both a magnitude and a direction associated with them. Two forces with the same magnitude but different directions are not equal forces. In general, an object can be acted on by several different forces or torques at any one time. The vector sum of all of the forces acting on a body is a single force called the net force. The vector sum of all the torques is a single torque called the net torque. If the net force (net torque) is equal to zero, the object is said to be in equilibrium. In equilibrium, because there is no net force (torque) on the object, then from Newton’s first law of motion, the object continues to move (rotate) at a constant speed. Some examples will help to explain the concept of equilibrium.

Vector Sum

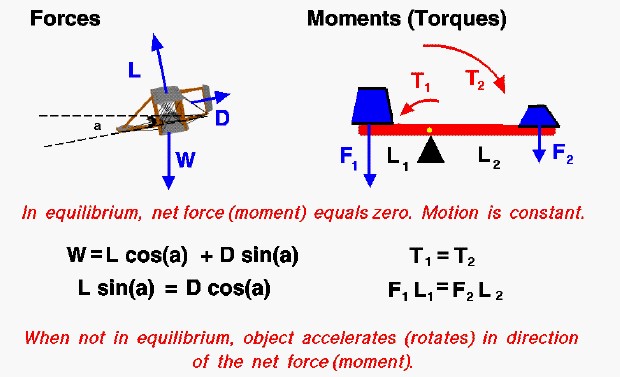
On the left of the slide we show a computer drawing of the Wright 1902 glider as it is descending. There are three forces acting on the glider; lift (L), drag (D), and weight (W). The weight is always directed towards the center of the earth, the lift is directed perpendicular to the flight path, and the drag is along the flight path. The flight path is inclined to the horizontal at an angle a. When the aircraft is in equilibrium, the vector sum of these three forces is equal to zero. Because it is a vector sum, there are two component equations (one vertical, one horizontal) which are shown below the graphic.

W = L * cos(a) + D * sin(a)

L * sin(a) = D * cos(a)

Force

The aircraft has a constant forward and downward velocity along the flight path. Notice that the lift, drag, and weight all continue to act on the aircraft. In equilibrium, the action of some forces are exactly balanced (cancelled out) by other forces. If the drag was to suddenly increase, (the pilot sticks his head up), then the aircraft would no longer be in equilibrium and the aircraft would begin to decelerate (accelerate in the direction of the drag).

Torque

On the right of the slide we consider a torque problem. Two weights are placed on opposite ends of a bar which is placed over a wedge as a pivot. The weight on the left (F1) is placed a distance (L1) from the pivot so it generates a torque (T1) which tends to rotate the bar counter-clockwise around the pivot.

T1 = F1 * L1

The weight on the right (F2) is placed a distance (L2) from the pivot, generating a torque (T2) which would rotate the bar clockwise.

T2 = F2 * L2

When the system is in equilibrium, T1 equals T2, the torques cancel each other out and the bar does not rotate in either direction.

T1 = T2

F1 * L1 = F2 * L2

If we were to add more weight to F2, then T2 would be greater than T1 and the bar would rotate clockwise. The system would no longer be in equilibrium.