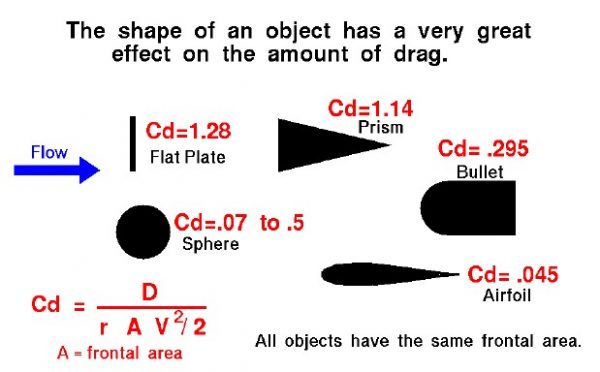
Effects of Shape on Drag

The drag coefficient is a number which aerodynamicists use to model all of the complex dependencies of drag on shape, inclination, and some flow conditions. The drag coefficient (Cd) is equal to the drag (D) divided by the quantity: density (r) times reference area (A) times one half of the velocity (V) squared.

Cd = D / (.5 * r * V^2 * A)

This slide shows some typical values of the drag coefficient for a variety of shapes. The values shown here were determined experimentally by placing models in a wind tunnel and measuring the amount of drag and the tunnel conditions of velocity and density. The drag equation was then used to produce the coefficient. The projected frontal area of each object was used as the reference area. A flat plate has Cd = 1.28, a wedge shaped prism with the wedge facing downstream has Cd = 1.14, a sphere has a Cd that varies from .07 to .5, a bullet has Cd = .295, and a typical airfoil has Cd = .045.

We can study the effect of shape on drag by comparing the values of drag coefficient for any two objects as long as the same reference area is used and the Mach number and Reynolds numbers are matched. All of the drag coefficients on this slide were produced in low speed (subsonic) wind tunnels and at similar Reynolds number, except as noted. A quick comparison shows that a flat plate gives the highest drag and a streamlined symmetric airfoil gives the lowest drag, by a factor of almost 30! Shape has a very large effect on the amount of drag produced. The drag coefficient for a sphere is given with a range of values because the drag on a sphere is highly dependent on Reynolds number. (Flow past a sphere, or cylinder, goes through a number of transitions with velocity. At very low velocity, a stable pair of vortices are formed on the downwind side. As velocity increases, the vortices become unstable and are alternately shed downstream. As velocity is increased even more, the boundary layer transitions to chaotic turbulent flow with vortices of many different scales being shed in a turbulent wake from the body. Each of these flow regimes produce a different amount of drag on the sphere.) Comparing the flat plate and the prism, and the sphere and the bullet, we see that the downstream shape can be modified to reduce drag.