Drag to Lift Ratio

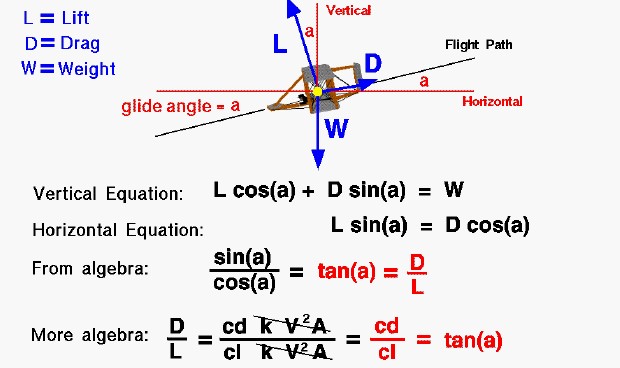
This slide shows the balance of forces on a descending Wright 1902 glider. The flight path of the glider is along the thin black line, which falls to the left. The flight path intersects the horizontal, thin, red ground line at an angle “a” called the glide angle.

There are three forces acting on the glider; lift, weight, and drag. The weight of the glider is given by the symbol “W” and is directed vertical, toward the center of the earth. The weight is then perpendicular to the horizontal red line drawn parallel to the ground and through the center of gravity. The drag of the glider is designated by “D” and acts along the flight path opposing the motion. Lift, designated “L,” acts perpendicular to the flight path. Using some geometry theorems on angles, perpendicular lines, and parallel lines, we see the glide angle “a” also defines the angle between the lift and the vertical, and between the drag and the horizontal.

Assuming that the forces are balanced (no acceleration of the glider), we can write two vector component equations for the forces. In the vertical direction, the weight (W) is equal to the lift (L) times the cosine (cos) of the glide angle (a) plus the drag (D) times the sine (sin) of the glide angle.

L * cos(a) + D * sin(a) = W

In the horizontal direction, the lift (L) times the sine (sin) of the glide angle (a) equals the drag (D) times the cosine (cos) of the glide angle.

L * sin(a) = D * cos(a)

If we use algebra to re-arrange the horizontal force equation we find that the drag divided by the lift is equal to the sine of the glide angle divided by the cosine of the glide angle. This ratio of trigonometric functions is equal to the tangent of the angle.

D / L = sin(a) / cos(a) = tan(a)

We can use the drag equation and the lift equation to relate the glide angle to the drag coefficient (cd) and lift coefficient (cl) that the Wrights measured in their wind tunnel tests.

D / L = cd / cl = tan(a)

During the operation of the drag balance the brothers made measurements of the effects of wing design on glide angle through the drag to lift ratio. The inverse of the drag to lift ratio is the L/D ratio which is an efficiency factor for aircraft design. The higher the L/D, the lower the glide angle, and the greater the distance that a glider can travel across the ground for a given change in height.